题目内容
20. 等腰△ABC中,腰长AB=8cm,BC=5cm,∠CBD=18°,AB的垂直平分线MN交AC于点D.
等腰△ABC中,腰长AB=8cm,BC=5cm,∠CBD=18°,AB的垂直平分线MN交AC于点D.(1)求△BCD的周长;
(2)求∠A的度数.
分析 (1)根据线段垂直平分线性质求出AD=BD,即可求出△BCD的周长=AC+BC,代入求出即可;
(2)设∠A=x°,根据等腰三角形性质推出∠ABD=∠A=x°,∠ABC=∠C=(x+18)°,得出关于x的方程,求出方程的解即可.
解答 解:(1)∵AB的垂直平分线MN交AC于点D,
∴AD=BD,
∵AB=AC=8cm,BC=5cm,
∴△BCD的周长为BC+BD+CD=BC+AD+DC=BC+AC=8cm+5cm=13cm;
(2)设∠A=x°,
∵AD=BD,
∴∠ABD=∠A=x°,
∵AB=AC,∠DCB=18°,
∴∠ABC=∠C=(x+18)°,
∵∠A+∠ABC+∠C=180°,
∴x+x+18+x+18=180,
∴x=48,
即∠A=48°.
点评 本题考查了解一元一次方程组,等腰三角形性质,三角形内角和定理,线段垂直平分线性质的应用,能求出AD=BD和得出关于x的方程是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
15.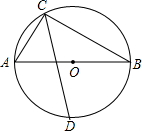 如图,AB为⊙O直径,C为⊙O上一点,∠ACB的平方线交⊙O于点D,若AB=10,AC=6,则CD的长为( )
如图,AB为⊙O直径,C为⊙O上一点,∠ACB的平方线交⊙O于点D,若AB=10,AC=6,则CD的长为( )
 如图,AB为⊙O直径,C为⊙O上一点,∠ACB的平方线交⊙O于点D,若AB=10,AC=6,则CD的长为( )
如图,AB为⊙O直径,C为⊙O上一点,∠ACB的平方线交⊙O于点D,若AB=10,AC=6,则CD的长为( )| A. | 7 | B. | 7$\sqrt{2}$ | C. | 8 | D. | 8$\sqrt{2}$ |
10.用一个平面去截一个圆锥,截面图形不可能是( )
| A. |  | B. |  | C. |  | D. |  |
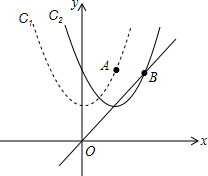 如图,已知抛物线C1:y=$\frac{1}{2}$x2+2上有一点A,点A的横坐标为2.将抛物线C1向右平移,使其顶点落在直线y=x上,此时抛物线记作为C2,点A的对应点记作B.
如图,已知抛物线C1:y=$\frac{1}{2}$x2+2上有一点A,点A的横坐标为2.将抛物线C1向右平移,使其顶点落在直线y=x上,此时抛物线记作为C2,点A的对应点记作B. 如图,AF=DC,BC∥EF,若添加条件∠A=∠D,则可利用“ASA”说明△ABC≌△DEF.
如图,AF=DC,BC∥EF,若添加条件∠A=∠D,则可利用“ASA”说明△ABC≌△DEF.