题目内容
7.(1)如图①,在正方形ABCD中,△AEF的顶点E、F分别在BC、CD上.AG⊥EF垂足为G,且AG=AB,求∠EAF的度数.(2)如图②在Rt△ABD中,∠BAD=90°,AB=AD,点M、N是BD上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE、AF于点M、N,如图③,若AB=12,BM=3$\sqrt{2}$,仔细观察图③与图②,利用(2)中结论,求MN的长.
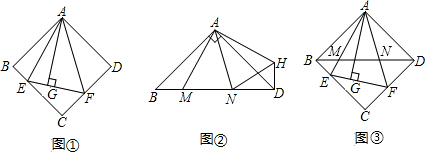
分析 (1)由HL证明△ABE≌△AGE、△AGF≌△ADF即可,只需证明一对全等,另一对同理可证;
(2)先证明△AMN≌△AHN,进而证明△NHD是直角三角形即可;
(3)算出BD的长,设MN=x,用x表示出DN,利用(2)中结论建立方程,解之即可.
解答 解:(1)如图①,
在Rt△ABE和Rt△AGE中,
$\left\{\begin{array}{l}{AB=AG}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△AGE(HL),
∴∠BAE=∠GAE,
同理∠GAF=∠DAF,
∴∠EAF=$\frac{1}{2}∠BAD$=45°;
(2)如图②,
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°,
由题意知△ABM≌ADH,
∴∠ADH=∠ABM=45°,AH=AM,
∴∠BDH=90°,
∵∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠DAN+∠DAH=45°,
即∠NAH=45°,
在△AMN和△AHN中,
$\left\{\begin{array}{l}{AM=AH}\\{∠MAN=∠HAN}\\{AN=AN}\end{array}\right.$,
∴△AMN≌△AHN(SAS),
∴HN=MN,
在Rt△NDH中,NH2=DH2+ND2,
∴MN2=BM2+DN2;
(3)如图③,
∵AB=12,
∴BD=12$\sqrt{2}$,
∵BM=3$\sqrt{2}$,
∴DM=9$\sqrt{2}$,
设MN=x,则DN=9$\sqrt{2}$-x,
由(2)中结论可知:MN2=BM2+DN2,
∴${x}^{2}=18+(9\sqrt{2}-x)^{2}$,
解得:x=5$\sqrt{2}$,
即MN=5$\sqrt{2}$.
点评 本题考查了旋转变换、全等三角形的判定与性质、等腰直角三角形的性质、正方形的性质、勾股定理等知识点,难度适中.本题是经典的“大角夹半角”模型,其基本证明方法必须熟练掌握.第(2)问当中所证明的结论可以认为是等腰直角三角形或正方形的重要性质,可直接记住,在解决一些相关的几何证明和计算时会有很大帮助.

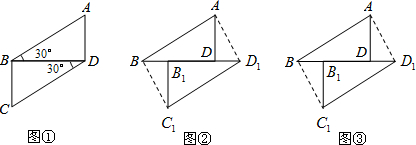
 如图,A,B两点分别位于一个池塘的两端,小聪明用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为14m,则A,B间的距离为28m.
如图,A,B两点分别位于一个池塘的两端,小聪明用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,找到AC,BC的中点D,E,并且测出DE的长为14m,则A,B间的距离为28m.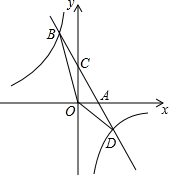 如图,在平面直角坐标系中,直线AB与x轴交于点A(1,0),与反比例函数在第二象限内的图象交于B(-1,n),连接BO,若S△AOB=2.
如图,在平面直角坐标系中,直线AB与x轴交于点A(1,0),与反比例函数在第二象限内的图象交于B(-1,n),连接BO,若S△AOB=2.