题目内容
4. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为$\sqrt{2}$.
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,取BC的中点P.当点B从点O向x轴正半轴移动到点M(2,0)时,则点P移动的路线长为$\sqrt{2}$.
分析 先过P作PD⊥x轴于D,作PE⊥y轴于E,根据△AEP≌△BDP(AAS),得出PE=PD,进而得到点P的运动路径是∠AOM的角平分线,再分别求得当点B与点O重合时,OP=$\frac{1}{2}$OC=$\frac{1}{2}\sqrt{2}$,当点B与点M重合时,OP=$\sqrt{2}$OD=$\frac{3}{2}\sqrt{2}$,进而得到点P移动的路线长.
解答 解:如图所示,过P作PD⊥x轴于D,作PE⊥y轴于E,则∠DPE=90°,∠AEP=∠BDP=90°,
连接AP,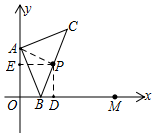
∵△ABC是等腰直角三角形,P是BC的中点,
∴AP=$\frac{1}{2}$BC=BP,且AP⊥BC,即∠APB=90°,
∴∠APE=∠BPD,
在△AEP和△BDP中,
$\left\{\begin{array}{l}{∠AEP=∠BDP}\\{∠APE=∠BPD}\\{AP=BP}\end{array}\right.$,
∴△AEP≌△BDP(AAS),
∴PE=PD,
∴点P的运动路径是∠AOM的角平分线,
如图所示,当点B与点O重合时,AB=AO=1,OC=$\sqrt{2}$,
∴OP=$\frac{1}{2}$OC=$\frac{1}{2}\sqrt{2}$;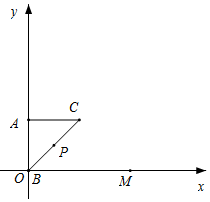
如图所示,当点B与点M重合时,过P作PD⊥x轴于D,作PE⊥y轴于E,连接OP,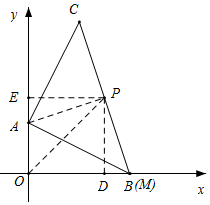
由△AEP≌△BDP,可得AE=BD,
设AE=BD=x,则OE=1+x,OD=2-x,
∵矩形ODPE中,PE=PD,
∴四边形ODPE是正方形,
∴OD=OE,即2-x=1+x,
解得x=$\frac{1}{2}$,
∴OD=2-$\frac{1}{2}$=$\frac{3}{2}$,
∴等腰Rt△OPD中,OP=$\sqrt{2}$OD=$\frac{3}{2}\sqrt{2}$,
∴当点B从点O向x轴正半轴移动到点M时,则点P移动的路线长为$\frac{3}{2}\sqrt{2}$-$\frac{1}{2}\sqrt{2}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题主要考查了全等三角形的判定与性质,正方形的判定,以及等腰直角三角形的性质的综合应用,解决问题的关键是作辅助线,构造全等三角形,得出点P的运动路径是∠AOM的角平分线.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 二次函数y=3(x-h)2+k的图象如图所示,下列判断正确的是( )
二次函数y=3(x-h)2+k的图象如图所示,下列判断正确的是( )| A. | h>0,k>0 | B. | h>0,k<0 | C. | h<0,k>0 | D. | h<0,k<0 |
| A. | -1 | B. | -$\frac{11}{3}$ | C. | 1 | D. | $\frac{11}{3}$ |
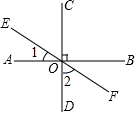 如图,直线AB、CD、EF相交于点O,其中AB⊥CD,∠1:∠2=3:6,则∠EOD=( )
如图,直线AB、CD、EF相交于点O,其中AB⊥CD,∠1:∠2=3:6,则∠EOD=( )| A. | 120° | B. | 130° | C. | 60° | D. | 150° |
 如图,函数y=$\frac{4}{x}$(x>0)图象上一点P的横坐标是4,过点P作直线l交x轴于点A,交y轴负半轴于点B,且OA=OB.
如图,函数y=$\frac{4}{x}$(x>0)图象上一点P的横坐标是4,过点P作直线l交x轴于点A,交y轴负半轴于点B,且OA=OB. 如图,已知△ABC是边长为2的等边三角形,试建立适当的直角坐标系,求出其各顶点的坐标.
如图,已知△ABC是边长为2的等边三角形,试建立适当的直角坐标系,求出其各顶点的坐标.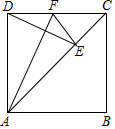 如图,将一张正方形纸片ABCD进行折叠,使得点D落在对角线AC上的点E处,折痕为AF.若AD=1,则DF=$\sqrt{2}$-1.
如图,将一张正方形纸片ABCD进行折叠,使得点D落在对角线AC上的点E处,折痕为AF.若AD=1,则DF=$\sqrt{2}$-1.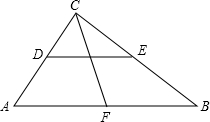 如图,在Rt△ABC中,∠ACB=90°,点F是AB的中点,CF=8cm,则中位线DE=8cm.
如图,在Rt△ABC中,∠ACB=90°,点F是AB的中点,CF=8cm,则中位线DE=8cm.