题目内容
 已知,如图△ABC中,I是内心,AI交BC于D,交△ABC的外接圆于点E,且∠B=60°,那么△IEC是等边三角形吗?说说你的理由.
已知,如图△ABC中,I是内心,AI交BC于D,交△ABC的外接圆于点E,且∠B=60°,那么△IEC是等边三角形吗?说说你的理由.考点:三角形的内切圆与内心
专题:
分析:根据内心是三角形的角的平分线的交点以及三角形的外角的性质求得∠EIC=60°,然后根据圆周角定理求得∠IEC的度数,根据有两个角是60度的三角形是等边三角形,即可证得.
解答: 解:△IEC是等边三角形.
解:△IEC是等边三角形.
理由是:∵△ABC中,∠BAC+∠ACB=180°-∠B=180°-60°=120°,
又∵I是△ABC的内心,则∠EAC=
∠BAC,∠ACI=
∠ACB,
∴∠EAC+∠ACI=
×120°=60°,
∴∠CAE=∠EAC+∠ACI=60°,
又∵∠AEC=∠B=60°,
∴△IEC是等边三角形.
 解:△IEC是等边三角形.
解:△IEC是等边三角形.理由是:∵△ABC中,∠BAC+∠ACB=180°-∠B=180°-60°=120°,
又∵I是△ABC的内心,则∠EAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EAC+∠ACI=
| 1 |
| 2 |
∴∠CAE=∠EAC+∠ACI=60°,
又∵∠AEC=∠B=60°,
∴△IEC是等边三角形.
点评:本题考查了三角形的内心的性质,以及圆周角定理,正确求得∠EIC的度数是关键.

练习册系列答案
相关题目
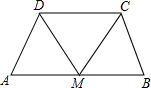 如图,点M是等腰梯形ABCD底边AB的中点,下列说法正确的是( )
如图,点M是等腰梯形ABCD底边AB的中点,下列说法正确的是( )| A、∠DAM=∠DCM |
| B、DM∥BC |
| C、△AMD≌△BMC |
| D、△AMD≌△DMC |
当ab>0时,y=ax2与y=ax+b的图象大致是( )
A、 |
B、 |
C、 |
D、 |
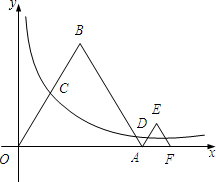 如图,已知等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
如图,已知等边△OAB和等边△AFE的一边都在x轴上,双曲线y=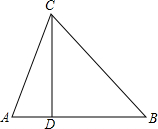 如图,已知△ABC中,AC=5,AB=6,BC=7,AB边上的高CD=3
如图,已知△ABC中,AC=5,AB=6,BC=7,AB边上的高CD=3 已知,如图,A,B分别为数轴上的两点,A点对应的数是-35,B点对应的数是85.
已知,如图,A,B分别为数轴上的两点,A点对应的数是-35,B点对应的数是85. 在图中,确定点A、B、C、D、E、F、G的坐标并说明点B和点F的位置关系.
在图中,确定点A、B、C、D、E、F、G的坐标并说明点B和点F的位置关系.