题目内容
如图,已知A(0,4),B(3,0),M(1,1),AB=5,MH⊥BO,P为x轴负半轴上一动点,作x轴关于PM对称轴的直线PQ交y轴于点Q,交AB于R,OD平分∠POQ交PM于D.
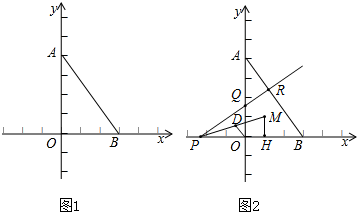
(1)求证:BM平分∠ABO;
(2)当
=
时,求
的值.

(1)求证:BM平分∠ABO;
(2)当
| OQ |
| PQ |
| 1 |
| 2 |
| OD |
| DM |
考点:一次函数综合题,三角形的外角性质,轴对称的性质,锐角三角函数的定义
专题:综合题
分析:(1)过点M作ME⊥y轴于点E,过点M作MF⊥AB于点F,连接MA、MO、MB,如图1,运用面积法求得MF=1,从而有MH=MF,然后根据角平分线的判定即可得到结论;
(2)由条件“
=
”可得∠QPO=30°,根据轴对称的性质可得∠OPM=15°,易证∠DOM=90°,在Rt△DOM中,根据三角形外角性质可得∠OMD=30°,然后只需运用三角函数的定义就可解决问题.
(2)由条件“
| OQ |
| PQ |
| 1 |
| 2 |
解答:(1)证明:过点M作ME⊥y轴于点E,过点M作MF⊥AB于点F,连接MA、MO、MB,如图1.
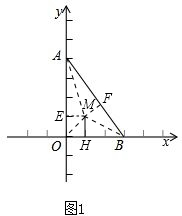
∵A(0,4),B(3,0),M(1,1),AB=5,MH⊥BO,
∴S△AOB=S△AOM+S△OBM+S△ABM
=
AO•ME+
OB•MH+
AB•MF
=
×4×1+
×3×1+
×5×MF
=
+
MF.
又∵S△AOB=
OB•OA=
×3×4=6,
∴
+
MF=6,
解得MF=1,
∴MH=MF.
∵MH⊥OB,MF⊥AB,
∴BM平分∠ABO.
(2)解:连接OM,如图2.
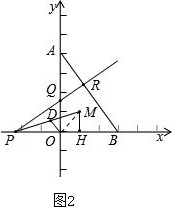
在Rt△POQ中,
当
=
时,有sin∠QPO=
=
,
∴∠QPO=30°.
∵直线PB与直线PR关于直线PM对称,
∴∠QPM=∠OPM=
∠QPO=15°.
∵OH=MH=1,∠OHM=90°,
∴∠HMO=∠MOH=45°.
∵OD平分∠POQ,
∴∠POD=∠QOD=
∠POQ=45°,
∴∠DOM=180°-45°-45°=90°.
在Rt△DOM中,
∵∠OMD=∠MOH-∠MPO=45°-15°=30°,
∴sin∠OMD=
=sin30°=
,
∴
的值为
.

∵A(0,4),B(3,0),M(1,1),AB=5,MH⊥BO,
∴S△AOB=S△AOM+S△OBM+S△ABM
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 7 |
| 2 |
| 5 |
| 2 |
又∵S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 7 |
| 2 |
| 5 |
| 2 |
解得MF=1,
∴MH=MF.
∵MH⊥OB,MF⊥AB,
∴BM平分∠ABO.
(2)解:连接OM,如图2.

在Rt△POQ中,
当
| OQ |
| PQ |
| 1 |
| 2 |
| OQ |
| PQ |
| 1 |
| 2 |
∴∠QPO=30°.
∵直线PB与直线PR关于直线PM对称,
∴∠QPM=∠OPM=
| 1 |
| 2 |
∵OH=MH=1,∠OHM=90°,
∴∠HMO=∠MOH=45°.
∵OD平分∠POQ,
∴∠POD=∠QOD=
| 1 |
| 2 |
∴∠DOM=180°-45°-45°=90°.
在Rt△DOM中,
∵∠OMD=∠MOH-∠MPO=45°-15°=30°,
∴sin∠OMD=
| OD |
| DM |
| 1 |
| 2 |
∴
| OD |
| DM |
| 1 |
| 2 |
点评:本题主要考查了轴对称的性质、三角形的外角性质、锐角三角函数的定义、角平分线的判定(到角两边距离相等的点在这个角的角平分线上)等知识,运用面积法求出MF的长是解决第(1)小题的关键,求得∠DOM=90°及∠OMD=30°是解决第(2)小题的关键.

练习册系列答案
相关题目
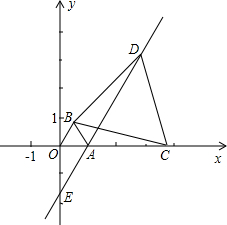 在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上一动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.
在平面直角坐标系中,O为坐标原点,点A坐标为(1,0),以OA为边在第一象限内作等边△OAB,C为x轴正半轴上一动点(OC>1),连接BC,以BC为边在第一象限内作等边△BCD,直线DA交y轴于E点.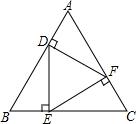 如图所示,△ABC是等边三角形,D、E、F分别在AB、BC、AC上,且DE⊥BC,EF⊥AC,FD⊥AB,试判断△DEF是否为等边三角形,并说时理由.
如图所示,△ABC是等边三角形,D、E、F分别在AB、BC、AC上,且DE⊥BC,EF⊥AC,FD⊥AB,试判断△DEF是否为等边三角形,并说时理由.