题目内容
15. 把直尺、三角尺和圆形螺母按如图所示放置于桌面上,∠CAB=60°,若量出AD=6cm,则圆形螺母的外直径是( )
把直尺、三角尺和圆形螺母按如图所示放置于桌面上,∠CAB=60°,若量出AD=6cm,则圆形螺母的外直径是( )| A. | 12cm | B. | 24cm | C. | 6$\sqrt{3}$cm | D. | 12$\sqrt{3}$cm |
分析 设圆形螺母的圆心为O,连接OD,OE,OA,如图所示:根据切线的性质得到AO为∠DAB的平分线,OD⊥AC,OD⊥AC,又∠CAB=60°,得到∠OAE=∠OAD=$\frac{1}{2}$∠DAB=60°,根据三角函数的定义求出OD的长,即为圆的半径,进而确定出圆的直径.
解答 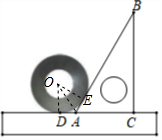 解:设圆形螺母的圆心为O,与AB切于E,连接OD,OE,OA,如图所示:
解:设圆形螺母的圆心为O,与AB切于E,连接OD,OE,OA,如图所示:
∵AD,AB分别为圆O的切线,
∴AO为∠DAB的平分线,OD⊥AC,OD⊥AC,又∠CAB=60°,
∴∠OAE=∠OAD=$\frac{1}{2}$∠DAB=60°,
在Rt△AOD中,∠OAD=60°,AD=6cm,
∴tan∠OAD=tan60°=$\frac{OD}{AD}$,即$\frac{OD}{6}$=$\sqrt{3}$,
∴OD=6$\sqrt{3}$cm,
则圆形螺母的直径为12$\sqrt{3}$cm.
故选D.
点评 此题考查了切线的性质,切线长定理,锐角三角函数定义,以及特殊角的三角函数值,熟练掌握性质及定理是解本题的关键.

练习册系列答案
相关题目
8.下列运算中,正确的是( )
| A. | a2•a3=a6 | B. | a2+a3=a6 | C. | a6÷a2=a4 | D. | 2(a+b)=2a+b |
9.如果M是五次多项式,N是五次多项式,那么M+N一定是( )
| A. | 十次多项式 | B. | 次数不高于五的整式 | ||
| C. | 五次多项式 | D. | 次数不低于五的整式 |
3.若△ABC与△DEF全等,且∠A=60°,∠B=70°,则∠D的度数不可能是( )
| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
10.如果在△ABC中,∠A=70°-∠B,则∠C等于( )
| A. | 140° | B. | 110° | C. | 70° | D. | 35° |
20.下列几何体中,主视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.把一个分数的分子扩大3倍,分母缩小3倍,这个分数的值( )
| A. | 不变 | B. | 扩大9倍 | C. | 缩小9倍 | D. | 无选项 |
 如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是121.75米.
如图,某游乐场的摩天轮(圆形转盘)上的点距离地面最大高度为160米,转盘直径为153米,旋转一周约需30分钟.某人从该摩天轮上到地面距离最近的点登舱,逆时针旋转20分钟,此时,他离地面的高度是121.75米.