题目内容
2.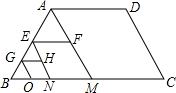 如图,四边形ABCD是等腰梯形,BC=2AD=4,过A作AM∥DC,得到第1个三角形,其平行于BC的中位线EF=1;过E作EN∥DC,得到第2个三角形,其平行于BC的中位线GH=$\frac{1}{2}$;过G作GO∥DC,得到第3个三角形,….按此规律作出第n个三角形,则其平行于BC的中位线长等于$\frac{1}{{2}^{n-1}}$.(用正整数n表示)
如图,四边形ABCD是等腰梯形,BC=2AD=4,过A作AM∥DC,得到第1个三角形,其平行于BC的中位线EF=1;过E作EN∥DC,得到第2个三角形,其平行于BC的中位线GH=$\frac{1}{2}$;过G作GO∥DC,得到第3个三角形,….按此规律作出第n个三角形,则其平行于BC的中位线长等于$\frac{1}{{2}^{n-1}}$.(用正整数n表示)
分析 根据题意分别表示出第1个三角形、第2个三角形、第3个三角形的中位线的长,根据规律写出第n个三角形平行于BC的中位线长即可.
解答 解:由题意得,第1个三角形的中位线EF=1=$\frac{1}{{2}^{1-1}}$;
第2个三角形中位线GH=$\frac{1}{2}$=$\frac{1}{{2}^{2-1}}$;
第3个三角形的中位线为$\frac{1}{4}$=$\frac{1}{{2}^{3-1}}$,
按此规律作出第n个三角形,则其平行于BC的中位线长等于$\frac{1}{{2}^{n-1}}$,
故答案为:$\frac{1}{{2}^{n-1}}$.
点评 本题考查的是三角形中位线定理和等腰梯形的性质,掌握三角形的中位线平行于第三边且等于第三边的一半是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
12. 如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
 如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
13.已知直角三角形的两条直角边的边长为3和4,则它的斜边长C是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 1<C<7 |
10.$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | -2 | D. | $\frac{\sqrt{2}}{2}$ |
7.下列多边形中,能够铺满地面的是( )
| A. | 正方形 | B. | 正五边形 | C. | 正七边形 | D. | 正八边形 |
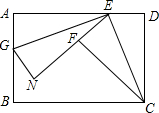 如图,在矩形ABCD中,E为AD边上一点,且AE=AB,把△CDE沿CE边翻折,点D落在点F处,G在AB边上,把△AEG沿EG边翻折,点A刚好落在EF的延长线上N点处.若BG=3,则FN的长为3.
如图,在矩形ABCD中,E为AD边上一点,且AE=AB,把△CDE沿CE边翻折,点D落在点F处,G在AB边上,把△AEG沿EG边翻折,点A刚好落在EF的延长线上N点处.若BG=3,则FN的长为3.