题目内容
1.某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
分析 (1)根据题意列方程组即可得到结论;
(2)①由题意列出关于x,y的方程即可;
②把函数关系式配方即可得到结果.
解答 解:(1)根据题意得:$\left\{\begin{array}{l}{2a+b=80}\\{3a+2b=135}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=25}\\{b=30}\end{array}\right.$;
(2)①由题意得:y=(x-20)【100-5(x-30)】
∴y=-5x2+350x-5000,
②∵y=-5x2+350x-5000=-5(x-35)2+1125,
∴当x=35时,y最大=1125,
∴销售单价为35元时,B商品每天的销售利润最大,最大利润是1125元.
点评 此题主要考查了二次函数的应用以及用配方法求出最大值,准确分析题意,列出y与x之间的二次函数关系式是解题关键.

练习册系列答案
相关题目
 如图,边长为1的正方形和直角边长为3的等腰直角三角形,开始它们在左边和下边重合,等腰直角三角形固定不动,把正方形自左向右平移直至移出等腰三角形外停止,设正方形移动的距离为x,两个图形重叠面积为y,则y关于x的函数图象大致是( )
如图,边长为1的正方形和直角边长为3的等腰直角三角形,开始它们在左边和下边重合,等腰直角三角形固定不动,把正方形自左向右平移直至移出等腰三角形外停止,设正方形移动的距离为x,两个图形重叠面积为y,则y关于x的函数图象大致是( )



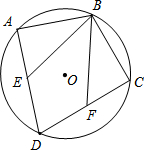 如图,四边形ABCD是⊙O的内接四边形,$\widehat{AB}$=$\widehat{BC}$,点E、F分别是弦AD、DC上的点.
如图,四边形ABCD是⊙O的内接四边形,$\widehat{AB}$=$\widehat{BC}$,点E、F分别是弦AD、DC上的点.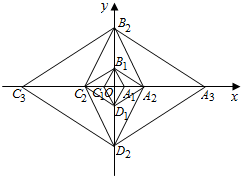 已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相较于点O,以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为(3n-1,0).
已知菱形A1B1C1D1的边长为2,∠A1B1C1=60°,对角线A1C1,B1D1相较于点O,以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2,再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2,…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点An的坐标为(3n-1,0).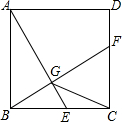 如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为$\sqrt{5}$-1.其中正确的说法是②④.(把你认为正确的说法的序号都填上)
如图,已知正方形ABCD的边长为2,E是边BC上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.下列说法:①AG>GE;②AE=BF;③点G运动的路径长为π;④CG的最小值为$\sqrt{5}$-1.其中正确的说法是②④.(把你认为正确的说法的序号都填上)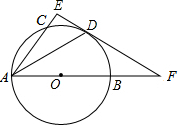 如图,AB是⊙O的直径,点C,D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于点E,与AB的延长线相交于点F.
如图,AB是⊙O的直径,点C,D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于点E,与AB的延长线相交于点F.