题目内容
13.现有四张分别标有1,2,2,3的卡片,它们除数字外完全相同,把卡片背面向上洗匀,从中随机抽取一张后放回,再背面朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率是$\frac{5}{8}$.分析 列表将所有等可能的结果列举出来,然后求得两次抽出的卡片所标数字不同的情况,再利用概率公式求解即可.
解答 解:列表得:
| 1 | 2 | 2 | 3 | |
| 1 | 11 | 12 | 12 | 13 |
| 2 | 21 | 22 | 22 | 23 |
| 2 | 21 | 22 | 22 | 23 |
| 3 | 31 | 32 | 32 | 33 |
∴两次抽出的卡片所标数字不同的概率是$\frac{10}{16}$=$\frac{5}{8}$.
故答案为:$\frac{5}{8}$.
点评 考查了列表与树状图的知识,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
3. 在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )
在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )
 在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )
在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )| A. | 2cm2 | B. | 1cm2 | C. | 0.5cm2 | D. | 0.25cm2 |
8.已知实数x1,x2满足x1+x2=7,x1x2=12,则以x1,x2为根的一元二次方程是( )
| A. | x2-7x+12=0 | B. | x2+7x+12=0 | C. | x2+7x-12=0 | D. | x2-7x-12=0 |
18.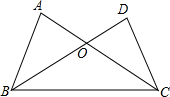 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )
 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )| A. | AB=DC,AC=DB | B. | AB=DC,∠ABC=∠DCB | C. | BO=CO,∠A=∠D | D. | AB=DC,∠DBC=∠ACB |
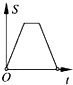
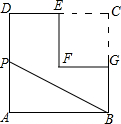 如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )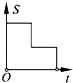
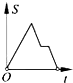
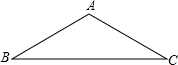 如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)
如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)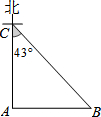 如图,海面上B、C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东43°.求A、B两岛之间的距离.(结果精确到0.1海里)
如图,海面上B、C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东43°.求A、B两岛之间的距离.(结果精确到0.1海里)