题目内容
17. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①$\frac{1}{4}$a+$\frac{1}{2}$b+c>0,②a<b,③4ac>b2,④abc>0.其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①$\frac{1}{4}$a+$\frac{1}{2}$b+c>0,②a<b,③4ac>b2,④abc>0.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据图象与坐标轴的交点情况判④,根据图象与x轴的交点个数判断③,根据顶点的坐标判断①,根据对称轴判断②.
解答 解:由于顶点的纵坐标大于0,所以当x=-$\frac{1}{2}$时,$\frac{1}{4}$a-$\frac{1}{2}$b+c>0,故①正确;
由于抛物线的对称轴x=-$\frac{b}{2a}$=-$\frac{1}{2}$,所以a=b,故②错误;
由于抛物线与x轴有两个交点,所以b2-4ac>0,故③错误;
由于抛物线开口向下,所以a<0,由于a=b<0,c=0,所以abc=0,故④错误.
点评 本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c);当b2-4ac>0,抛物线与x轴有两个交点;当b2-4ac=0,抛物线与x轴有一个交点;当b2-4ac<0,抛物线与x轴没有交点.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
9.若m>n,则下列不等式中一定成立的是( )
| A. | m+2<n+3 | B. | 2m<3n | C. | a-m<a-n | D. | ma2>na2 |

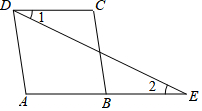 如图,已知AD∥BC,∠1=∠2,试说明∠A=∠C.
如图,已知AD∥BC,∠1=∠2,试说明∠A=∠C.