题目内容
14.如图1,直角△OAB(其中O为直角顶点,∠OAB=30°)的直角边OA与线段OP重合在同一根射线OM上,它们绕着点O同时进行转动,△OAB沿着逆时针方向,线段OP沿着顺时针方向,已知OA,OP分别与OM的夹角关于时间t的变化图象如图2所示,则t=$\frac{3}{7}$或3或$\frac{57}{7}$(单位:秒)时,有AB∥OP.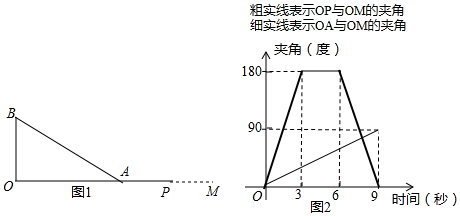
分析 先由图2中的信息得出OP的旋转速度和旋转情况,△OAB的旋转速度和旋转情况,分三种情况计算.
解答 当0<t≤3时,Ⅰ、如图1,
此时,△OAB和OP同时旋转,旋转到如图1的位置时,BA∥OP,
∴∠AOP=∠A=30°,
∴60°t+10°t=30°,
∴t=$\frac{3}{7}$;
Ⅱ、如图2,
△OAB和OP同时旋转到如图2的位置时,AB∥OP,
∴∠BOP=∠B=90°-∠A=60°,
∴△OAB和OP同时旋转了360°-∠BOP-∠AOB=360°-60°-90°=210°,
∴60°t+10°t=210°,
∴t=3,
当3<t<6时,此时OP不动,△OAB按原速度,原方向旋转,不存在AB∥OP的情况,
当6≤t≤9时,如图3,
此时,△OAB按原速度原方向旋转,OP也按原速度原方向旋转,旋转到如图3的位置时,BA∥OP,
∴∠AOP=30°,OP旋转了60°(t-3),△OAB旋转了10°t,
∴60°(t-3)+10°t=360°+∠AOP=390°,
∴t=$\frac{57}{7}$.
故答案为$\frac{3}{7}$或3或$\frac{57}{7}$.
点评 此题主要考查了三角形和线段的旋转,旋转的旋转,平行线的性质,解本题的关键是从图2中找到信息求出它们的旋转速度.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
6.下列命题正确的是( )
| A. | 相等的角是对顶角 | B. | a、b、c是直线,若a∥b,b∥c,则a∥c | ||
| C. | 同位角相等 | D. | a、b、c是直线,若a⊥b,b⊥c,则a⊥c |
4.下列因式分解正确的是( )
| A. | -2x2-2=-2(x+1)(x-1) | B. | x2-4x+4=(x-2)2 | C. | x2+9=(x+3)2 | D. | x2+3x+1=x(x+3)+1 |
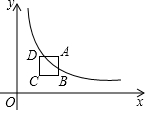 在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),如图1,若双曲线y=$\frac{5}{x}$(x>0)与此正方形的边有交点,则a的取值范围是$\sqrt{5}$≤a≤$\sqrt{5}$+1.
在平面直角坐标系的第一象限内,边长为1的正方形ABCD的边均平行于坐标轴,A点的坐标为(a,a),如图1,若双曲线y=$\frac{5}{x}$(x>0)与此正方形的边有交点,则a的取值范围是$\sqrt{5}$≤a≤$\sqrt{5}$+1.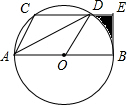 如图所示,CD是⊙O的弦,AB是⊙O的直径,且CD∥AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E.
如图所示,CD是⊙O的弦,AB是⊙O的直径,且CD∥AB,连接AC,AD,OD,其中AC=CD,过点B的切线交CD的延长线于E.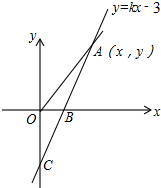 如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB
如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB