题目内容
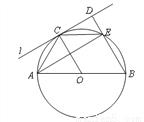
如图,PA、PB分别切⊙O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( )

A. 60° B. 75° C. 105° D. 120°
C 【解析】如图,连接AO,OB, 因为PA,PB分别切圆O于A,B两点, 所以∠PAO=∠PBO=90°, 所以∠AOB=180°-∠P=150°, 设点E是优弧AB上一点, 由圆周角定理可知, ∠E=75°, 由圆内接四边形的对角互补可知, ∠ACB=180°-∠E=105°, 故选C.
练习册系列答案
相关题目


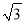 B. 9(
B. 9(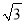 -1) C. 9(
-1) C. 9(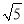 -1) D. 9
-1) D. 9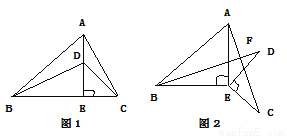
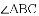
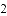
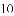
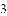
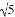 ,
,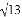 .
.