题目内容
如图1,将一副三角尺,如图放置在桌面上,让三角尺OAB的30°角顶点与三角板OCD的直角顶点重合,边OA与OC重合,固定三角尺OCD不动,把三角尺OAB绕着顶点O顺时针转动,直到边OB落在桌面上为止.
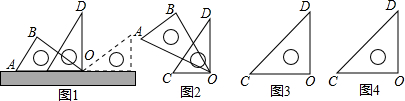
(1)当三角板OAB转动了多少度时,即∠COA= °时,OB恰好平分∠COD;
(2)如图2,当三角板OAB转动了32°,即∠COA=32°时,求∠BOD的度数;
(3)在转动过程中,若∠BOD=20°,请在如图3的两图中分别画出∠AOB的大致位置,并求出∠COA的度数.

(1)当三角板OAB转动了多少度时,即∠COA=
(2)如图2,当三角板OAB转动了32°,即∠COA=32°时,求∠BOD的度数;
(3)在转动过程中,若∠BOD=20°,请在如图3的两图中分别画出∠AOB的大致位置,并求出∠COA的度数.
考点:角的计算,角平分线的定义
专题:
分析:(1)由∠COD=90°,可知当OB恰好平分∠COD时,∠COB=45°,而∠COB=∠COA+∠BOA,故可得∠COA=15°;
(2)由∠COD=90°,∠COD=∠COA+∠BOA+∠BOD,即可得到∠BOD的度数;
(3)分OB在OD的左边或右边两种情况讨论即可求解.
(2)由∠COD=90°,∠COD=∠COA+∠BOA+∠BOD,即可得到∠BOD的度数;
(3)分OB在OD的左边或右边两种情况讨论即可求解.
解答:解:(1)∵∠COD=90°,
∴OB恰好平分∠COD时,∠COB=45°,
∵∠COB=∠COA+∠BOA,
∴∠COA=45°-30°=15°,
故答案为:15°;
(2)如图,∵∠COD=90°,∠COD=∠COA+∠BOA+∠BOD,∠COA=32°,∠AOB=30°
∴∠BOD=90°-32°-30°=28°;
(3)如图3,
图3中第一个图形的∠COA=90°-20°-30°=40°
第二个图形的∠COA=90°-(30°-20°)=80°;
∴OB恰好平分∠COD时,∠COB=45°,
∵∠COB=∠COA+∠BOA,
∴∠COA=45°-30°=15°,
故答案为:15°;
(2)如图,∵∠COD=90°,∠COD=∠COA+∠BOA+∠BOD,∠COA=32°,∠AOB=30°
∴∠BOD=90°-32°-30°=28°;
(3)如图3,
图3中第一个图形的∠COA=90°-20°-30°=40°

第二个图形的∠COA=90°-(30°-20°)=80°;
点评:本题主要考查角的有关计算,通过观察图形得到角之间的和差关系式解决本题的关键.

练习册系列答案
相关题目
 如图,它是一个正方体的展开图,若此正方体的相对面上的数互为相反数,则a-(b-c)=
如图,它是一个正方体的展开图,若此正方体的相对面上的数互为相反数,则a-(b-c)=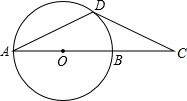 如图,点D是半径为R的⊙O上一点.
如图,点D是半径为R的⊙O上一点.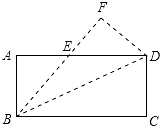 如图,矩形ABCD中,BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E.
如图,矩形ABCD中,BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E.