题目内容
2.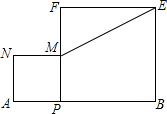 如图,线段AB=10,点P是AB的动点,分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF,连结ME,则ME的最小值是2$\sqrt{5}$.
如图,线段AB=10,点P是AB的动点,分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF,连结ME,则ME的最小值是2$\sqrt{5}$.
分析 设ME=y,FM=x,根据正方形的性质和勾股定理列出y2关于x的二次函数关系式,求二次函数的最值即可.
解答 解:ME=y,AP=x,则
y2=(10-x)2+(10-2x)2=5(x-6)2+20.
∵0≤x≤10,
∴当x=6式,y2最小值=20,
∴y最小值=2$\sqrt{5}$.
故答案是:2$\sqrt{5}$.
点评 本题考查了二次函数的最值.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法.

练习册系列答案
相关题目
10.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表.已知购进60双甲种运动鞋与50双乙种运动鞋共用10000元
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)超过21000元,且不超过22000元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)超过21000元,且不超过22000元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
17.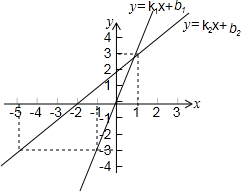 一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
 一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )
一次函数y=k1x+b1和y=k2x+b2的图象如图所示,自变量为x时对应的函数值分别为y1,y2.若-3<y1<y2,则x的取值范围是( )| A. | x<-1 | B. | -5<x<1 | C. | -5<x<-1 | D. | -1<x<1 |
14.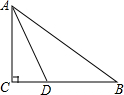 如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )
 如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )
如图,在△ABC中,∠C=90°,AD平分∠CAB,已知CD=3,BD=5,则下列结论中错误的是( )| A. | AC=6 | B. | AD=7 | C. | BC=8 | D. | AB=10 |
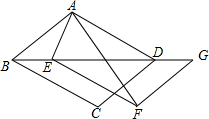 如图,在平行四边形ABCD中,∠ABD=30°,AB=4,BD=5$\sqrt{3}$,将△BCD沿方向平移BD,得到△EFG.
如图,在平行四边形ABCD中,∠ABD=30°,AB=4,BD=5$\sqrt{3}$,将△BCD沿方向平移BD,得到△EFG.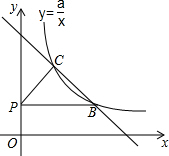 如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次 函数y=kx+b与反比例函数y=$\frac{a}{x}$(a>0,x>0)的图象的两个交点,且点B(m,2).当点P的坐标为(0,2)时,PC=BC,且∠PCB=90°.
如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次 函数y=kx+b与反比例函数y=$\frac{a}{x}$(a>0,x>0)的图象的两个交点,且点B(m,2).当点P的坐标为(0,2)时,PC=BC,且∠PCB=90°. 如图,直线a、b相交于点O,∠1=50°,则∠2=50度.
如图,直线a、b相交于点O,∠1=50°,则∠2=50度.