题目内容
3.当分式$\frac{x-2}{x+2}$的值是正数、负数、0时,求x的取值范围.分析 根据$\frac{x-2}{x+2}$的值是正数时,则分子与分母一定同号,分同正与同负两种情况;
分式的值是负数,则分子与分母一定异号,应分分子是正数,分母是负数和分子是负数,分母是正数两种情况进行讨论;
分式的值是0,则分子等于0,分母不等于0,从而得出答案.
解答 解:∵分式$\frac{x-2}{x+2}$的值是正数,
∴$\frac{x-2}{x+2}$>0,解得x>2或x<-2,
∴当x>2或x<-2时,分式的值为正数;
∵分式$\frac{x-2}{x+2}$的值是负数,
∴$\frac{x-2}{x+2}$<0,解得-2<x<2;
∴当-2<x<2时,分式的值为负数;
∴当x=2时,分式的值为0.
点评 本题主要考查了分式的值的正负,以及值是0的条件,对这些条件的理解是解决本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
13.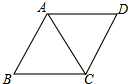 如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )
如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )
 如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )
如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长为( )| A. | 3 | B. | 3$\sqrt{3}$ | C. | 6 | D. | 6$\sqrt{3}$ |
 到直线l1、l2的距离相等的点的轨迹是什么?
到直线l1、l2的距离相等的点的轨迹是什么?