题目内容
如图，在⊙O中，∠AOB=120°， |
| BC |
|
| AC |
| A、15° | B、20° |
| C、30° | D、40° |
考点：圆周角定理,圆心角、弧、弦的关系
专题：探究型
分析：连接OC，先根据∠AOB=120°可得出
=120°，再由
=2
可得出
=
，故可得出∠AOC的度数，由圆周角定理即可得出结论．
|
| AB |
|
| BC |
|
| AC |
|
| AC |
| 1 |
| 3 |
|
| AB |
解答：
解：连接OC，
∵∠AOB=120°，
∴
=120°，
∵
=2
，
∴
=
=
×120°=40°，
∴∠AOC=40°，
∴∠ADC=
∠AOC=
×40°=20°．
故选B．
解：连接OC，∵∠AOB=120°，
∴
|
| AB |
∵
|
| BC |
|
| AC |
∴
|
| AC |
| 1 |
| 3 |
|
| AB |
| 1 |
| 3 |
∴∠AOC=40°，
∴∠ADC=
| 1 |
| 2 |
| 1 |
| 2 |
故选B．
点评：本题考查的是圆周角定理及圆心角、弧、弦的关系，根据题意作出辅助线，构造出圆心角是解答此题的关键．
练习册系列答案
天天向上口算本系列答案
相关题目
已知两圆的半径分别为6和4，圆心距为2，则两圆的位置关系是（ ）
| A、相交 | B、内含 | C、外切 | D、内切 |
计算（
-1）（
+1）的结果是（ ）
| 2 |
| 2 |
| A、1 | ||
B、
| ||
C、
| ||
D、3+2
|
如图，在四边形ABCD中，∠ABC=∠ADC=90°，AC⊥BD于O，求证：AC平分∠BAD．
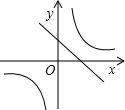
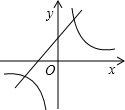
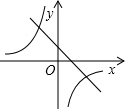
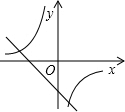
下列坐标表示的点中，不在反比例函数y=
的图象上的是（ ）
| 6 |
| x |
| A、（-2，-3） |
| B、（-1，-6） |
| C、（-0.5，12） |
| D、（1.5，4） |