题目内容
16.从△ABC的顶点A向∠ABC,∠ACB的平分线引垂线,垂足分别是D,E.求证:DE∥BC.分析 如图,延长AE交BC延长线于F,延长AD交CB延长线于G,构建△AGF的中位线,利用三角形中位线定理来证得结论.
解答  证明:如图,延长AE交BC延长线于F,延长AD交CB延长线于G,
证明:如图,延长AE交BC延长线于F,延长AD交CB延长线于G,
∵BE平分∠ABF,
∴∠ABE=∠FBE.
∵在△ABE与△FBE中,$\left\{\begin{array}{l}{∠ABE=∠FBE}\\{BE=BE}\\{∠AEB=∠FEB=90°}\end{array}\right.$,
∴△ABE≌△FBE(ASA),
∴AE=FE,
∴点E是边AF的中点.
同理,△ACD≌△GCD(ASA),
∴AD=GD,
∴点D是边AG的中点.
∴DE是△AGF的中位线,
∴DE∥GF,则DE∥BC.
点评 本题考查了三角形中位线定理,等腰三角形的判定与性质.解答该题的难点是通过作辅助线,构建全等三角形,从而推知DE是△AGF的中位线.

练习册系列答案
相关题目
 如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.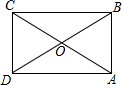 如图,在矩形ABCD中,对角线AC、BD相交于点O,OA=AB,OD=3cm,则矩形ABCD的面积为9$\sqrt{3}$cm2.
如图,在矩形ABCD中,对角线AC、BD相交于点O,OA=AB,OD=3cm,则矩形ABCD的面积为9$\sqrt{3}$cm2.