题目内容
11.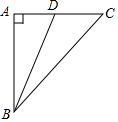 如图,等腰直角△ABC中,∠A=90°,AD:DC=1:2,求∠DBC的三角函数值.
如图,等腰直角△ABC中,∠A=90°,AD:DC=1:2,求∠DBC的三角函数值.
分析 先过点D作DE⊥BC于E,得到∠CDE=∠C=45°,再设AD=k,则CD=2k,AB=3k,根据勾股定理求得Rt△ABD中,BD=$\sqrt{10}$k,Rt△CDE中,DE=CE=$\sqrt{2}$k,Rt△ABC中,BC=3$\sqrt{2}$k,BE=2$\sqrt{2}$k,最后计算∠DBC的三角函数值.
解答 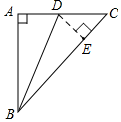 解:如图所示,过点D作DE⊥BC于E,则∠CDE=∠C=45°,
解:如图所示,过点D作DE⊥BC于E,则∠CDE=∠C=45°,
∵等腰直角△ABC中,∠A=90°,AD:DC=1:2,
∴设AD=k,则CD=2k,AB=3k,
∴Rt△ABD中,BD=$\sqrt{10}$k,
Rt△CDE中,DE=CE=$\sqrt{2}$k,
Rt△ABC中,BC=3$\sqrt{2}$k,
∴BE=2$\sqrt{2}$k,
∴在Rt△BDE中,sin∠DBC=$\frac{DE}{DB}$=$\frac{\sqrt{2}k}{\sqrt{10}k}$=$\frac{\sqrt{5}}{5}$,
cos∠DBC=$\frac{BE}{BD}$=$\frac{2\sqrt{2}k}{\sqrt{10}k}$=$\frac{2}{5}\sqrt{5}$,
tan∠DBC=$\frac{DE}{BE}$=$\frac{\sqrt{2}k}{2\sqrt{2}k}$=$\frac{1}{2}$,
cot∠DBC=2.
点评 本题主要考查了等腰直角三角形的性质和解直角三角形的综合应用,解决问题的关键是作辅助线构造等腰直角三角形.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
16.已知$\overrightarrow{b}$=-2$\overrightarrow{a}$($\overrightarrow{a}$、$\overrightarrow{b}$均为非零向量),那么下列判断错误的是( )
| A. | |${\overrightarrow b}$|=2|$\overrightarrow a}$| | B. | 2$\overrightarrow a+\overrightarrow b=0$ | C. | $\overrightarrow b∥\overrightarrow a$ | D. | $\overrightarrow b≠\overrightarrow a$ |
19.下列运算正确的是( )
| A. | -2-25=-23 | B. | a-(b+c-d)=a-b+c+d | C. | 2πx2-3x2=(2π-3)x2 | D. | (-3)2×2=-12 |
16.某次考试中,A、B、C、D、E五位同学的数学、英语成绩如表所示:(单位:分)
(1)求这五位同学数学成绩的标准差和极差(结果可保留根号);
(2)为了比较同一学生不同学科考试成绩的好与差,可采用“标准分”进行比较,标准分大的成绩更好;已知:标准分=(个人成绩-平均分)÷成绩的标准差.
请通过计算说明B同学在这次考试中,数学与英语哪个学科考得更好?
| A | B | C | D | E | 平均分 | 标准差 | 极差 | |
| 英语 | 82 | 88 | 94 | 85 | 76 | 85 | 6 | 18 |
| 数学 | 71 | 72 | 69 | 68 | 70 | 70 | $\sqrt{2}$ | 4 |
(2)为了比较同一学生不同学科考试成绩的好与差,可采用“标准分”进行比较,标准分大的成绩更好;已知:标准分=(个人成绩-平均分)÷成绩的标准差.
请通过计算说明B同学在这次考试中,数学与英语哪个学科考得更好?

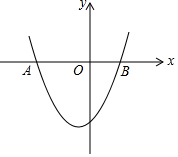 如图,已知抛物线y=x2+x-6与x轴两个交点分别是A、B(点A在点B的左侧).
如图,已知抛物线y=x2+x-6与x轴两个交点分别是A、B(点A在点B的左侧).