题目内容
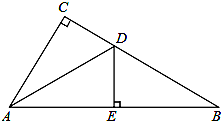
已知在△ABC中，∠C=90°，D为AB上的中点，连接C、D，求证：AD=CD=BD．
考点：直角三角形斜边上的中线
专题：证明题
分析：以D为圆心，AD为半径作圆，由∠C=90°，所以点C在圆上，所以CD=AD=BD．
解答：证明：
如图，以D为圆心，AD为半径作圆，
∵∠ACB=90°，
∴∠ACB为直径AB所对的圆周角，
即点C在圆上，
∴CD=DA=BD．
如图，以D为圆心，AD为半径作圆，
∵∠ACB=90°，
∴∠ACB为直径AB所对的圆周角，
即点C在圆上，
∴CD=DA=BD．
点评：本题主要考查圆周角定理的应用，利用条件作出以D为圆心AD为半径的圆证明C在圆上是解题的关键．
练习册系列答案
相关题目
下列各式中，不成立的是（ ）
| A、|-5|=5 |
| B、-|5|=-5 |
| C、|-5|=|5| |
| D、-|5|=5 |
如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．若∠B=30°，CD=1，求BD的长．
如图，在平面直角坐标系中，A（-1，5），B（-1，0），C（-4，3）．已知代数式x-2y的值是3，则代数式6y-3x+13值是（ ）
| A、1 | B、4 | C、7 | D、不能确定 |