题目内容
5.我们知道$\sqrt{2}$≈1.414,于是我们说:“$\sqrt{2}$的整数部分为1,小数部分则可记为$\sqrt{2}$-1”.则:(1)$\sqrt{2}$-3的整数部分为-1,小数部分则可记为$\sqrt{2}$-2;
(2)已知3+$\sqrt{31}$的小数部分为a,7-$\sqrt{31}$的小数部分为b,那么a+b的值是1;
(3)已知x是$\sqrt{10}$的整数部分,y是$\sqrt{10}$的小数部分,求${(y-\sqrt{10})^{x-1}}$的平方根.
分析 (1)先估算出$\sqrt{2}$-3的取值范围,进而可得出结论;
(2)估算出3+$\sqrt{31}$与7-$\sqrt{31}$的取值范围,故可得出a与b的值,代入代数式进行计算即可;
(3)先估算出$\sqrt{10}$的取值范围,故可得出x、y的值,代入代数式进行计算即可.
解答 解:(1)∵1<2<4,
∴1<$\sqrt{2}$<3,
∴1-3<$\sqrt{2}$-3<0,即-2<$\sqrt{2}$-3<0,
∴$\sqrt{2}$-3的整数部分是-1,小数部分是$\sqrt{2}$-2.
故答案为:-1,$\sqrt{2}$-2;
(2)∵25<31<36,
∵5<$\sqrt{31}$<6,
∴8<3+$\sqrt{31}$<9,
∴3+$\sqrt{31}$的小数部分是$\sqrt{31}$-5,即a=$\sqrt{31}$-5;
同理,∵25<31<36,
∵-6<-$\sqrt{31}$<-5,
∴1<7-$\sqrt{31}$<2
∴7-$\sqrt{31}$的小数部分为7-$\sqrt{31}$-1=6-$\sqrt{31}$,即b=6-$\sqrt{31}$,
∴a+b=$\sqrt{31}$-5+6-$\sqrt{31}$=1.
故答案为:1;
(3)∵9<10<16,
∴3<$\sqrt{10}$<4,
∴$\sqrt{10}$的整数部分是3,小数部分是$\sqrt{10}$-3,即a=3,y=$\sqrt{10}$-3,
∴${(y-\sqrt{10})^{x-1}}$=($\sqrt{10}$-3-$\sqrt{10}$)3-1=(-3)2=9,
∵±$\sqrt{9}$=±3,
∴${(y-\sqrt{10})^{x-1}}$的平方根是±3.
点评 本题考查的是估算无理数的大小,熟知估算无理数大小要用逼近法是解答此题的关键.

| A. | -2 | B. | 2 | C. | -2 或2 | D. | 0 |
 如图,数轴上表示$\sqrt{3}$,2的对应点分别为A、B,点B关于点A的对称点为C,则点C表示的实数为( )
如图,数轴上表示$\sqrt{3}$,2的对应点分别为A、B,点B关于点A的对称点为C,则点C表示的实数为( )| A. | $\sqrt{3}$-2 | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-1 | D. | $2\sqrt{3}$-2 |
| A. | $\frac{1}{5}$ | B. | -5 | C. | 5 | D. | -$\frac{1}{5}$ |
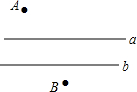 如图,幸福小区A和超市B位于公路的两侧,现要在公路上建一座天桥,天桥建在何处可使小区A的人到超市B购物最近?(假定公路的两边是平行的直线,天桥与公路垂直)
如图,幸福小区A和超市B位于公路的两侧,现要在公路上建一座天桥,天桥建在何处可使小区A的人到超市B购物最近?(假定公路的两边是平行的直线,天桥与公路垂直)