题目内容
【题目】如图，正方形
的边长是9，点
是
边上的一个动点，点
是
边上一点，
，连接
，把正方形沿折叠，使点
，
分别落在点
，
处，当点落在线段
上时，线段
的长为__________．
【答案】2
【解析】
当D'落在线段BC上时，连接ED、ED'、DD'，由折叠性质可知D'和D关于EF对称，即EF垂直平分DD'，得出D E=D'E.求出DF=D'F=CD-CF=5， 
.得出BD'=BC-CD'=6，设AE=x，则BE=9-x，在Rt△AED和Rt△BED'中，由勾股定理列方程解答即可．
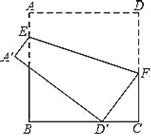
解：当D落在线段BC上时，如图1:连接ED、E D'.、DD'
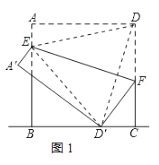
由折叠性质可知，D'和D关于EF对称，即EF垂直平分DD'.
∴ DE=D'E，
∵正方形ABCD的边长是9，
∴AB=BC=CD=AD=9.
∵CF=4，
∴DF=D'F=CD-CF=9-4=5
∴
∴BD'=BC-CD'=6
设AE=x，则BE=9-x，
在Rt△AED和Rt△BED'中.由勾股定理得：
92+x2=（9-x）2+62，
解得：x=2，即AE=2．
练习册系列答案
名校课堂系列答案
相关题目
