题目内容
6．
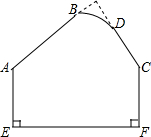如图所示的模板，规定：AB、CD的延长线应相交成80°的角，因交点不在模板上，不便测量，工人师傅测得∠BAE=124°，∠DCF=155°，此时AB，CD的延长线相交所成的角是否符合规定？为什么？
分析 AB与CD的延长线交于点G，根据五边形内角和等于540°，结合垂直的定义，计算可求∠G的度数，然后根据题意进行判断．
解答 解：AB与CD的延长线交于点G，如图，
∵AE⊥EF，CF⊥EF，
∴∠E=∠F=90°，
∵∠BAE=124°，∠DCF=155°，
∴∠G=540°-（124°+155°+90°×2）
=540°-459°
=81°，
∵81°≠80°，
∴不符合规定．
点评 考查了多边形内角和定理和垂直的定义，关键是根据图形求出要求的角的度数．
练习册系列答案
阅读快车系列答案
相关题目
15．
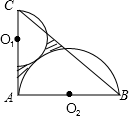如图，△ABC是直角边长为6的等腰直角三角形，直角边AB是半圆O2的直径，半圆O1过C点且与半圆O2相切，则图中阴影部分的面积是（ ）
如图，△ABC是直角边长为6的等腰直角三角形，直角边AB是半圆O2的直径，半圆O1过C点且与半圆O2相切，则图中阴影部分的面积是（ ）| A． | $\frac{46-13π}{4}$ | B． | $\frac{32-9π}{2}$ | C． | $\frac{23-13π}{4}$ | D． | $\frac{54-13π}{4}$ |
16．某学习小组8名同学的体重分别是35、50、45、42、36、38、40、42（单位：kg），这组数据的平均数和众数分别为（ ）
| A． | 41、42 | B． | 41、41 | C． | 36、42 | D． | 36、41 |