题目内容
5. 如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为250($\sqrt{3}$+1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为250($\sqrt{3}$+1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
分析 根据题意,在△ABC中,∠ABC=30°,∠BAC=45°,AB=250($\sqrt{3}$+1)米,是否受到影响取决于C点到AB的距离,因此求C点到AB的距离,作CD⊥AB于D点.
解答 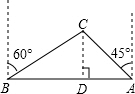 解:过点C作CD⊥AB于D,
解:过点C作CD⊥AB于D,
∵∠BAC=45°,
∴CD=AD,
∵∠ABC=30°,
∴BC=2CD,
设AD=CD=x,
∴BC=2x,
BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=$\sqrt{3}$x,
∵BD+AD=AB=250($\sqrt{3}$+1)(米),
即$\sqrt{3}$x+x=250($\sqrt{3}$+1),
∴x=250,
250米>200米.
答:在此路段修建铁路,油库C是不会受到影响.
点评 此题考查了解直角三角形及勾股定理的应用,用到的知识点是方向角,关键是根据题意画出图形,作出辅助线,构造直角三角形,“化斜为直”是解三角形的基本思路,常需作垂线(高),原则上不破坏特殊角(30°、45°、60°).

练习册系列答案
相关题目
17.下列计算正确的是( )
| A. | x2+2x=3x2 | B. | x6÷x2=x3 | C. | x2•(2x3)=2x5 | D. | (3x2)2=6x2 |
18.下列计算正确的是( )
| A. | a3-a2=a | B. | a2•a3=a6 | C. | (3a)3=9a3 | D. | (a2)2=a4 |
17.下列计算正确的是( )
| A. | x2+x2=x4 | B. | 2x3-x3=x3 | C. | x2•x3=x6 | D. | (x2)3=x5 |
 )﹣3+
)﹣3+ ﹣(
﹣( )0
)0 ,则运算
,则运算 的最小值为( )
的最小值为( )