题目内容
6.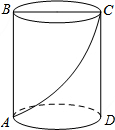 如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,求昆虫爬行的最短路程.
如图,一圆柱体的底面周长为24cm,高AB为16cm,BC是上底面的直径.一只昆虫从点A出发,沿着圆柱的侧面爬行到点C,求昆虫爬行的最短路程.
分析 先将图形展开,再根据两点之间线段最短可知AC长即昆虫爬行的最短路程,然后利用勾股定理求解,即可求得答案.
解答  解:如图,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高.
解:如图,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,C是边的中点,矩形的宽即高.
∵AD=$\frac{1}{2}$×24=12(cm),CD=16cm,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=20(cm).
∴昆虫爬行的最短路程为:20cm.
点评 此题考查了最短路径问题,注意将圆柱体展成平面图是解此题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
1.若点P(b-3,-2b)在y轴上,则点P的坐标为( )
| A. | (0,-6) | B. | (-6,0) | C. | (0,6) | D. | (6,0) |
18.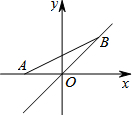 如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
 如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )
如图,点A的坐标为(-1,0),点B在直线y=x上运动,已知直线y=x与x轴的夹角为45°,则当线段AB最短时,点B的坐标为( )| A. | (0,0) | B. | ($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$) |
 白日登山望烽火,黄昏饮马傍交河.诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A点出发,奔向小河旁边的P点饮马,饮马后再到B点宿营,若A、B到水平直线L(L表示小河)的距离分别是2,1,AB两点之间水平距离是4,则AP+PB最小值=5.
白日登山望烽火,黄昏饮马傍交河.诗中隐含着一个有趣的数学问题:诗中将军在观望烽火之后从山脚上的A点出发,奔向小河旁边的P点饮马,饮马后再到B点宿营,若A、B到水平直线L(L表示小河)的距离分别是2,1,AB两点之间水平距离是4,则AP+PB最小值=5.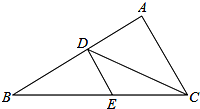 如图所示,在△ABC中,CD平分∠ACB,DE∥AC.
如图所示,在△ABC中,CD平分∠ACB,DE∥AC.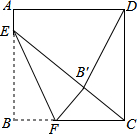 如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为16或4$\sqrt{5}$.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为16或4$\sqrt{5}$.