题目内容
 如图,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.求:
如图,在四边形ABDC中,∠A=90°,AB=9,AC=12,BD=8,CD=17.求:(1)BC的长;
(2)四边形ABDC的面积.
分析:(1)连接BC,根据勾股定理可求得BC的长.
(2)根据勾股定理的逆定理可得到△BCD也是直角三角形,从而求得△ABC与△BCD的面积和即得到了四边形ABDC的面积.
(2)根据勾股定理的逆定理可得到△BCD也是直角三角形,从而求得△ABC与△BCD的面积和即得到了四边形ABDC的面积.
解答: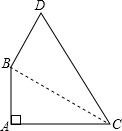 解:(1)连接BC,
解:(1)连接BC,
∵∠A=90°,AB=9,AC=12
∴BC=15,
(2)∵BC=15,BD=8,CD=17
∴BC2+BD2=CD2
∴△BCD是直角三角形
∴S四边形ABCD=S△BCD+S△ABC=
×15×8+
×9×12=114
 解:(1)连接BC,
解:(1)连接BC,∵∠A=90°,AB=9,AC=12
∴BC=15,
(2)∵BC=15,BD=8,CD=17
∴BC2+BD2=CD2
∴△BCD是直角三角形
∴S四边形ABCD=S△BCD+S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查学生对勾股定理及三角形的面积公式的理解及运用.

练习册系列答案
相关题目
 16、如图,在四边形ABCD中,已知AB与CD不平行,∠ABD=∠ACD,请你添加一个条件:
16、如图,在四边形ABCD中,已知AB与CD不平行,∠ABD=∠ACD,请你添加一个条件: 20、如图,在四边形ABCD中,BD是线段AC的垂直平分线,已知△ABD的周长是30cm,四边形ABCD的周长为36cm,求线段BD的长.
20、如图,在四边形ABCD中,BD是线段AC的垂直平分线,已知△ABD的周长是30cm,四边形ABCD的周长为36cm,求线段BD的长. 3、如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=76°,∠BDC=28°,延长BD至点E,使得DE=DC,连接AE,则∠DBC的度数为( )
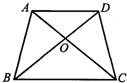
3、如图,在四边形ABCD中,AB=AC,∠ABD=60°,∠ADB=76°,∠BDC=28°,延长BD至点E,使得DE=DC,连接AE,则∠DBC的度数为( ) 如图,在四边形ABCD中,AC与BD相交于点O,S△ABD:S△CBD=3:2,则OA:OC的值为
如图,在四边形ABCD中,AC与BD相交于点O,S△ABD:S△CBD=3:2,则OA:OC的值为 如图,在四边形ABCD中,已知AB不平行于CD,∠ABD=∠DCA,请你添加一个条件:
如图,在四边形ABCD中,已知AB不平行于CD,∠ABD=∠DCA,请你添加一个条件: