题目内容
16.(1)解不等式$\frac{x-1}{3}$≤1-x,并把解集表示在数轴上.(2)解不等式组$\left\{\begin{array}{l}{3x+1>4}\\{4-2x≥0}\end{array}\right.$,并把解集表示在数轴上.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1即可;
(2)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答 解:(1)$\frac{x-1}{3}$≤1-x,
x-1≤3(1-x),
x-1≤3-3x,
x+3x≤3+1,
4x≤4,
x≤1,
在数轴上表示不等式的解集为: ;
;
(2)$\left\{\begin{array}{l}{3x+1>4①}\\{4-2x≥0②}\end{array}\right.$
∵解不等式①得:x>1,
解不等式②得:x≤2,
∴不等式组的解集为1<x≤2,
在数轴上表示不等式的解集为: .
.
点评 本题考查了解一元一次不等式组,解一元一次不等式,在数轴上表示不等式组的解集的应用,解此题的关键是能根据不等式的性质正确解一元一次不等式和能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
相关题目
6.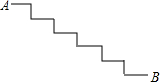 如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于( )
如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于( )
 如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于( )
如图,是台阶的示意图.已知每个台阶的宽度都是30cm,每个台阶的高度都是15cm,连接AB,则AB等于( )| A. | 195cm | B. | 200cm | C. | 205cm | D. | 210cm |
11.雾和霾是不同的,雾是空气中的水蒸气液化形成的,而造成霾的主凶之一是空气中的浮尘,我国在2012年开始试点使用PM2.5标准来检测空气质量,是指大气中直径大于2.5微米的颗粒物,也称为可入肺颗粒物,对人的呼吸系统会造成极大的危害,你知道2.5微米合( )米(1微米=0.000001米)
| A. | 2.5×10-6 | B. | 2.5×10-5 | C. | 25×10-6 | D. | 2.5×10-7 |
8.下列说法中正确的是( )
| A. | 三角形的角平分线、中线、高均在三角形内部 | |
| B. | 三角形中至少有一个内角不小于60° | |
| C. | 直角三角形仅有一条高 | |
| D. | 三角形的外角大于任何一个内角 |
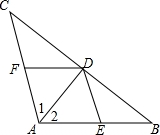 如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB 交AC于F.试判断四边形AEDF是怎样的四边形?并说明理由.
如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB 交AC于F.试判断四边形AEDF是怎样的四边形?并说明理由.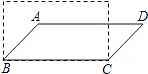 如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最大内角等于150°.
如图,若将四根木条钉成的矩形木框变成平行四边形ABCD的形状,并使其面积为矩形面积的一半,则这个平行四边形的最大内角等于150°.