题目内容
4.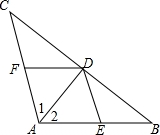 如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB 交AC于F.试判断四边形AEDF是怎样的四边形?并说明理由.
如图,AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB 交AC于F.试判断四边形AEDF是怎样的四边形?并说明理由.
分析 首先利用平行四边形的判定得出四边形AEDF是平行四边形,根据角平分线的定义可得∠1=∠2,再根据两直线平行,内错角相等可得∠ADF=∠2,从而∠ADF=∠1,得出AF=DF,得解.
解答 解:四边形AEDF是菱形,
理由:∵DF∥AB,DE∥AC.
∴四边形AEDF是平行四边形,
∵DF∥AB,
∴∠2=∠ADF,
∵AD是角平分线,
∴∠1=∠2,
∴∠ADF=∠1,
∴AF=DF.
∴四边形AEDF是菱形.
点评 本题考查了平行线的性质、角平分线的定义、菱形的判定与性质,准确识图并熟记性质是解题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
12.若$\frac{x-y}{13}$=$\frac{y}{7}$,则$\frac{x+y}{y}$=( )
| A. | $\frac{13}{7}$ | B. | $\frac{20}{7}$ | C. | $\frac{27}{7}$ | D. | 无法确定 |
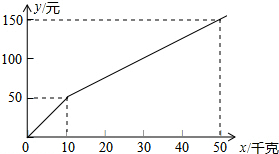 某种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格打折,因此付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如果所示,下列四种说法:
某种子公司以一定价格销售“黄金1号”玉米种子,如果一次购买10千克以上(不含10千克)的种子,超过10千克的那部分种子的价格打折,因此付款金额y(单位:元)与一次购买种子数量x(单位:千克)之间的函数关系如果所示,下列四种说法:
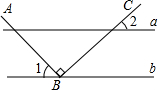 如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=44°,求∠2的度数.
如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=44°,求∠2的度数. 已知AB∥CD,BC∥DE,BF平分∠ABC,DG平分∠EDC,求证:DG⊥BF.
已知AB∥CD,BC∥DE,BF平分∠ABC,DG平分∠EDC,求证:DG⊥BF.