题目内容
6．
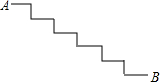如图，是台阶的示意图．已知每个台阶的宽度都是30cm，每个台阶的高度都是15cm，连接AB，则AB等于（ ）| A． | 195cm | B． | 200cm | C． | 205cm | D． | 210cm |
分析 作出直角三角形后分别求得直角三角形的两直角边的长后即可利用勾股定理求得斜边AB的长．
解答 
解：如图，由题意得：AC=15×5=75cm，
BC=30×6=180cm，
故AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{7{5}^{2}+18{0}^{2}}$=195cm．
故选A．
点评 本题考查了勾股定理的应用，解题的关键是从实际问题中抽象出直角三角形，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
16．当x取任意实数时，下列各根式有意义的是（ ）
| A． | $\sqrt{x+1}$ | B． | $\sqrt{\frac{x-1}{2}}$ | C． | $\sqrt{\frac{3}{{x}^{2}}}$ | D． | $\sqrt{|x|+1}$ |
17．如果点P（a，b）在x轴上，那么点Q（ab，-1）在（ ）
| A． | y轴的正半轴上 | B． | y轴的负半轴上 | C． | x轴的正半轴上 | D． | x轴的负半轴上 |
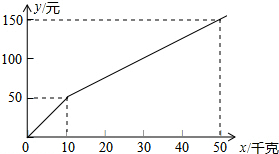某种子公司以一定价格销售“黄金1号”玉米种子，如果一次购买10千克以上（不含10千克）的种子，超过10千克的那部分种子的价格打折，因此付款金额y（单位：元）与一次购买种子数量x（单位：千克）之间的函数关系如果所示，下列四种说法：
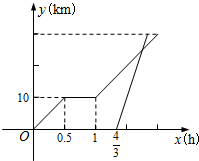周末，小明骑电动自行车从家里出发到野外郊游．从家出发0.5小时后到达甲地，游玩一段时间后按原速前往乙地．小明离家1小时20分钟后，妈妈驾车沿相同路线前往乙地．如图是他们离家的路程y（km）与小明离家时间x（h）的函数图象．已知妈妈驾车的速度是小明骑电动自行车速度的3倍．
11．已知|3a-2b-12|+（a+2b+4）2=0．则（ ）
| A． | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=2}\\{b=-3}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{a=-3}\\{b=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ |
18．若a=0.32，b=（-$\frac{1}{3}$）-2，c=（-$\frac{1}{3}$）0，则（ ）
| A． | a＜b＜c | B． | b＜c＜a | C． | a＜c＜b | D． | b＜a＜c |