题目内容
13.若关于x的一元二次方程a(x-x1)(x-x2)=0(a≠0且x1≠x2)与关于x的一元一次方程dx+e=0(d≠0)有一个公共解x=x1,且方程a(x-x1)(x-x2)+dx+e=0只有一个解,则( )| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
分析 由x=x1是方程a(x-x1)(x-x2)=0和dx+e=0的一个公共解,可得出x=x1是方程a(x-x1)(x-x2)+dx+e=0的一个解,根据根与系数的关系即可得出x1+x1=-$\frac{-(a{x}_{1}+a{x}_{2}-d)}{a}$,整理后即可得出结论.
解答 解:∵关于x的一元二次方程a(x-x1)(x-x2)=0与关于x的一元一次方程dx+e=0有一个公共解x=x1,
∵x=x1是方程a(x-x1)(x-x2)+dx+e=0的一个解.
∵方程a(x-x1)(x-x2)+dx+e=ax2-(ax1+ax2-d)x+ax1•x2+e=0只有一个解,
∴x1+x1=-$\frac{-(a{x}_{1}+a{x}_{2}-d)}{a}$,
整理得:d=a(x2-x1).
故选B.
点评 本题考查了一元二次方程的解以及根与系数的关系,根据根与系数的关系找出x1+x1=-$\frac{-(a{x}_{1}+a{x}_{2}-d)}{a}$是解题的关键.

练习册系列答案
相关题目
1. 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AE⊥AB交BC于点E.若S△ABC=m2+9n2,S△ADE=mn,则m与n之间的数量关系是( )
如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AE⊥AB交BC于点E.若S△ABC=m2+9n2,S△ADE=mn,则m与n之间的数量关系是( )
 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AE⊥AB交BC于点E.若S△ABC=m2+9n2,S△ADE=mn,则m与n之间的数量关系是( )
如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AE⊥AB交BC于点E.若S△ABC=m2+9n2,S△ADE=mn,则m与n之间的数量关系是( )| A. | m=3n | B. | m=6n | C. | n=3m | D. | n=6m |
8.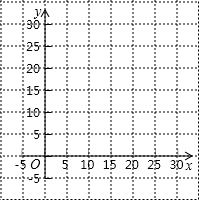 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
(1)根据表中数据在平面直角坐标系中描出实数x,y的对应点,用平滑曲线连接这些点,并观察所得的图象,猜测y与x之间的函数关系,并求出该函数关系式:
(2)设经营此笔记本的日销售利润为w元,试求出w与x之间的函数关系式;
(3)当日销售单价为8元时,求日销售利润是多少元?
 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:(1)根据表中数据在平面直角坐标系中描出实数x,y的对应点,用平滑曲线连接这些点,并观察所得的图象,猜测y与x之间的函数关系,并求出该函数关系式:
| x(元) | 3 | 4 | 5 | 6 |
| y(个) | 20 | 15 | 12 | 10 |
(3)当日销售单价为8元时,求日销售利润是多少元?
2. 如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
 如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )| A. | 16cm2 | B. | 20cm2 | C. | 80cm2 | D. | 160cm2 |

 如图,菱形ABCD的对角线AC、BD相交于点O,AC=8,BD=6,则此菱形的周长为20.
如图,菱形ABCD的对角线AC、BD相交于点O,AC=8,BD=6,则此菱形的周长为20.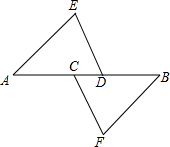 如图:点C,D在AB上,且AC=BD,AE=FB,DE=FC.求证:△ADE≌△BCF.
如图:点C,D在AB上,且AC=BD,AE=FB,DE=FC.求证:△ADE≌△BCF.