题目内容
3.(1)先化简,再求值:1-$\frac{x-2y}{x+y}$÷$\frac{{{x^2}-4xy+4{y^2}}}{{{x^2}-{y^2}}}$,其中x=-2,y=$\frac{1}{2}$(2)解分式方程:$\frac{x}{1-x}$=$\frac{5}{3x-3}$+1.
分析 (1)原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的减法法则计算得到最简结果,把x与y的值代入计算即可求出值;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=1-$\frac{x-2y}{x+y}$•$\frac{(x+y)(x-y)}{(x-2y)^{2}}$=1-$\frac{x-y}{x-2y}$=$\frac{x-2y-x+y}{x-2y}$=-$\frac{y}{x-2y}$,
当x=-2,y=$\frac{1}{2}$时,原式=$\frac{1}{6}$;
(2)方程两边乘3(x-1),得-3x=5+3(x-1),
解得:x=-$\frac{1}{3}$,
检验:当x=-$\frac{1}{3}$时,3(x-1)≠0,
则原分式方程的解为x=-$\frac{1}{3}$.
点评 此题考查了解分式方程,以及分式的化简求值,解分式方程注意要检验.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
13. 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
(1)当桌子上放有x个碟子时,碟子的高度是1.8x+1.2;(用含x的式子表示)
(2)分别从三个方向看桌子上摆放的四摞碟子的形状如上图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后碟子的高度.
 学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:
学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如下表:| 碟子的个数 | 碟子的高度 (单位:cm) |
| 1 | 3 |
| 2 | 3+1.8 |
| 3 | 3+3.6 |
| 4 | 3+5.4 |
| … | … |
(2)分别从三个方向看桌子上摆放的四摞碟子的形状如上图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后碟子的高度.
11.用科学记数法表示0.00056,正确的是( )
| A. | 5.6×10-3 | B. | 5.6×10-4 | C. | 5.6×10-5 | D. | 0.56×10-3 |
18.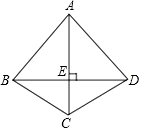 如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
 如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )| A. | AC平分∠BCD | B. | AB=BD | C. | △BEC≌△DEC | D. | BC=DC |
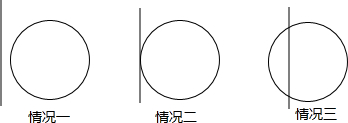
 如图,用直尺和圆规,在△ABC中画AB边上的中线.(保留作图痕迹)
如图,用直尺和圆规,在△ABC中画AB边上的中线.(保留作图痕迹)