题目内容
7.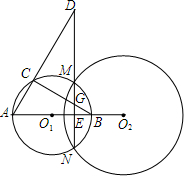 圆O1、圆O2相交于M、N,点D是NM延长线上一点,O1O2延长线交圆O1于B、A,AD交圆O1于C,MN交O1O2于E,交BC于G,求证:EM2=ED•EG.
圆O1、圆O2相交于M、N,点D是NM延长线上一点,O1O2延长线交圆O1于B、A,AD交圆O1于C,MN交O1O2于E,交BC于G,求证:EM2=ED•EG.
分析 首先根据两圆的连心线垂直平分公共弦,可知O1O2⊥MN,且ME=NE,结合相交弦定理得ME2=AE•BE,然后再证明△BGE∽△DAE,由相似三角形的性质可得到AE•BE=EG•DE,从而可证得ME2=DE•EG.
解答 解:∵O1O2是两圆的连心线,MN是公共弦,
∴O1O2⊥MN,且ME=NE.
由相交弦定理可知:AE•BE=ME•NE,
又∵ME=NE,
∴ME2=AE•BE.
∵AB是⊙O1的直径,
∴∠ACB=90°
∴∠CAB+∠ABC=90°.
∵AB⊥DE,
∴∠EAD+∠D=90°
∴∠D=∠EBG.
在△BGE和△DAE中,∠D=∠EBG,∠GEB=∠DEA=90°
∴△BGE∽△DAE.
∴$\frac{EG}{AE}=\frac{EB}{DE}$.
∴AE•BE=EG•DE.
∴ME2=DE•EG.
点评 本题主要考查的是相交弦定理和相似三角形的性质和判定,证得ME2=AE•BE,AE•BE=EG•DE是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.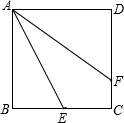 如图,正方形ABCD的边长为8,点E在BC边的中点,点F在CD上且AE平分∠BAF.则AF的等于( )
如图,正方形ABCD的边长为8,点E在BC边的中点,点F在CD上且AE平分∠BAF.则AF的等于( )
 如图,正方形ABCD的边长为8,点E在BC边的中点,点F在CD上且AE平分∠BAF.则AF的等于( )
如图,正方形ABCD的边长为8,点E在BC边的中点,点F在CD上且AE平分∠BAF.则AF的等于( )| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
 如图CD是⊙O的直径,弦AB⊥CD,垂足为E,连BC,若AB=2$\sqrt{2}$cm,∠BCD=22°30′,则⊙O的半径为2cm.
如图CD是⊙O的直径,弦AB⊥CD,垂足为E,连BC,若AB=2$\sqrt{2}$cm,∠BCD=22°30′,则⊙O的半径为2cm.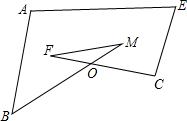 课堂上,老师提出一个问题:如图,求∠A+∠ABO+∠M+∠F+∠ECF+∠E的度数.独立思考:
课堂上,老师提出一个问题:如图,求∠A+∠ABO+∠M+∠F+∠ECF+∠E的度数.独立思考: