题目内容
19．用十字相乘法分解因式：（1）3x2+5x-2；
（2）5m2+6mn-8n2．
分析 （1）把二次项系数3分解成两个因数3，1的积3，把常数项-2分解成两个因数-1和2，积是-2，并使3×2-1正好是一次项5，那么可以直接写成结果：3x2+5x-2=（3x-1）（x+2）；
（2）把二次项系数a分解成两个因数a1，a2的积a1•a2，把常数项c分解成两个因数c1，c2的积c1•c2，并使a1c2+a2c1正好是一次项b，那么可以直接写成结果：ax2+bx+c=（a1x+c1）（a2x+c2）．
解答 解：（1）原式=（3x-1）（x+2）；
（2）原式=（m+2n）（5m-4n）．
点评 本题考查十字相乘法分解因式，运用十字相乘法分解因式时，要注意观察，尝试，并体会它实质是二项式乘法的逆过程．
练习册系列答案
走进文言文系列答案
相关题目
10．
a，b是有理数，它们在数轴上的对应点的位置如所示：把a，-a，b，-b按照由小到大的顺序排列是（ ）
a，b是有理数，它们在数轴上的对应点的位置如所示：把a，-a，b，-b按照由小到大的顺序排列是（ ）| A． | -b＜-a＜b＜a | B． | -a＜b＜-b＜a | C． | -a＜-b＜b＜a | D． | -b＜-a＜b＜a |
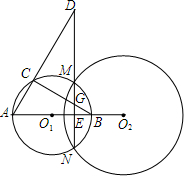圆O1、圆O2相交于M、N，点D是NM延长线上一点，O1O2延长线交圆O1于B、A，AD交圆O1于C，MN交O1O2于E，交BC于G，求证：EM2=ED•EG．
如图，三角形ABC中，线段AF与射线DE交于点P，其中点D、F在BC上，点E在射线AC上，点P′在射线DE上，平移三角形ABC，使点P移动到点P′．