题目内容
17．已知y是x的二次函数，y与x的部分对应值如下表：| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 0 | 3 | 4 | 3 | … |
分析 利用表格中的对称性得：抛物线与x轴另一个交点为（3，0），可得结论．
解答 解：由表格得：二次函数的对称轴是直线x=$\frac{0+2}{2}$=1．
∵抛物线与x轴另一个交点为（-1，0），
∴抛物线与x轴另一个交点为（3，0），
∴该二次函数图象向左平移3个单位，图象经过原点；或该二次函数图象向右平移1个单位，图象经过原点．
故答案为3．
点评 本题考查了二次函数图象与几何变换-平移，根据平移的原则：左加右减进行平移；也可以利用数形结合的思想画图解决．
练习册系列答案
阅读快车系列答案
相关题目
7．4条直线两两相交，有（ ）个交点．
| A． | 1个 | B． | 4个 | C． | 6个 | D． | 以上都有可能 |
8．某数学兴趣小组利用假期50天社会实践参与了一家网店经营，了解到一种成本为20元/件的新型商品在第x天销售的相关信息如表所示．
（1）设销售该新型商品的当天利润为y元，当1≤x＜30时，
①求出y与x的函数关系式；
②问销售该商品第几天时，当天利润最大，最大利润是多少？
（2）该商品在销售过程中，第1天至第30天当天利润不低于1200元？$（\sqrt{3}≈1.73）$．
| 时间第x（天） | 1≤x＜30 | 30≤x≤50 |
| 售价（元/件） | x+30 | 60 |
| 每天销量（件） | 100-2x | |
①求出y与x的函数关系式；
②问销售该商品第几天时，当天利润最大，最大利润是多少？
（2）该商品在销售过程中，第1天至第30天当天利润不低于1200元？$（\sqrt{3}≈1.73）$．
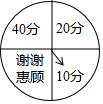“五一”假日期间，某网店为了促销，设计了一种抽奖送积分活动，在该网店网页上显示如图所示的圆形转盘，转盘被均等的分成四份，四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样．参与抽奖的顾客只需用鼠标点击转盘，指针就会在转动的过程中随机的停在某个扇形区域，指针指向扇形上的积分就是顾客获得的奖励积分，凡是在活动期间下单的顾客，均可获得两次抽奖机会，求两次抽奖顾客获得的总积分不低于30分的概率．
如图所示，若∠1=82°，∠2=98°，∠3=77°，则∠4=77°．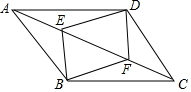
已知：如图，E、F是平行四边形ABCD的对角线AC上的两点，AE=CF．求证：EB∥DF．
6．下列计算正确的是（ ）
| A． | a3-a2=a | B． | a2•a3=a6 | C． | （a-b）2=a2-b2 | D． | （-a2）3=-a6 |