题目内容
19．
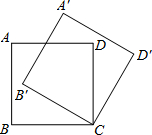如图，将边长为6的正方形ABCD绕点C顺时针旋转30°得到正方形A′B′CD′，则点A的旋转路径长为$\sqrt{2}π$．（结果保留π）
分析 如图，作辅助线；首先求出AC的长度，然后运用弧长公式即可解决问题．
解答 
解：如图，连接AC、A′C．
∵四边形ABCD为边长为6的正方形，
∴∠B=90°，AB=BC=6，
由勾股定理得：AC=6$\sqrt{2}$，
由题意得：∠ACA′=30°，
∴点A的旋转路径长=$\frac{30π•6\sqrt{2}}{180}$=$\sqrt{2}π$，
故答案为$\sqrt{2}π$．
点评 该题以正方形为载体，以旋转变换为方法，以考查旋转变换的性质为核心构造而成；解题的关键是将求点A 的旋转路径长问题，转化为求弧长问题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
9．
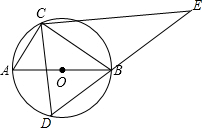如图，AB是⊙O的直径，点C在⊙O上，且tan∠ABC=$\frac{1}{2}$，D是⊙O上的一个动点（C，D两点位于直径AB的两侧），连接CD，过点C作CE⊥CD交DB的延长线于点E．若⊙O的半径是$\sqrt{5}$，则线段CE长度的最大值是（ ）
如图，AB是⊙O的直径，点C在⊙O上，且tan∠ABC=$\frac{1}{2}$，D是⊙O上的一个动点（C，D两点位于直径AB的两侧），连接CD，过点C作CE⊥CD交DB的延长线于点E．若⊙O的半径是$\sqrt{5}$，则线段CE长度的最大值是（ ）| A． | 2$\sqrt{5}$ | B． | 5$\sqrt{5}$ | C． | $\frac{16\sqrt{5}}{5}$ | D． | 4$\sqrt{5}$ |
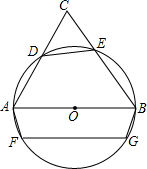已知，如图，以△ABC的边AB作直径的⊙O，分别交AC、BC于点D、E，弦FG∥AB，S△CDE：S△ABC=1：4，DE=5cm，FG=8cm，求梯形AFGB的面积．
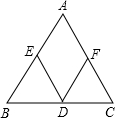如图，在△ABC中，DE∥AC，DF∥AB．
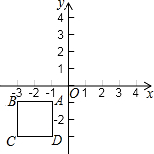如图，在直角坐标系xOy中，正方形ABCD顶点A（-1，-1）、B（-3，-1）．我们规定“把正方形ABCD先沿x轴翻折，再向右平移2个单位”称为一次变换．若正方形ABCD经过2015次这样的变换得到正方形A2015B2015C2015D2015，则点B2015的坐标是（4027，1）．
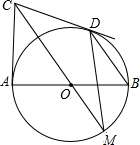如图，AB为⊙O的直径，CA、CD分别切⊙O于A、D，CO的延长线交⊙O于M，连BD、DM．