Question

【题目】如图，在中，以为直径的交边于点，过点作于点，交于点，连结

（1）求证：

（2）当时，求的直径．

Answer 1

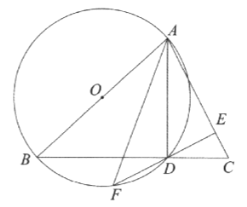
【答案】（1）见解析；（2）

【解析】

（1）利用直径所对的角是直角求得∠BDA=90°，由∠B=∠F，利用等角的余角相等，证得∠BAD=∠FAE，从而证得结论；

（2）连结BF，利用勾股定理求得AC=，再证得△ABF∽△ACD，得到，即可求解．

（1）∵AB是圆O的直径，

∴∠BDA=90°，

∴∠BAD+∠B=90°，

∵EF⊥AC，

∴∠FAE+∠F=90°，

∵∠B=∠F，

∴∠BAD=∠FAE，

∴∠BAD－∠DAF=∠FAE－∠DAF，

即：∠BAF=∠DAC；

（2）连结BF，

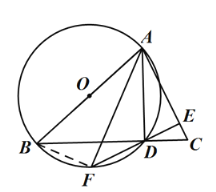
∵AB是圆O的直径，

∴∠BFA=90°，

∵∠BDA=90°，

∴∠ADC=180°-∠BDA=90°，

∴AC=，

∴∠BFA=∠ADC=90°，

由（1）得：∠BAF=∠DAC，

∴△ABF∽△ACD，

∴，即，

∴．