题目内容
6.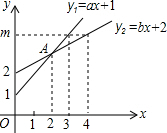 已知射线y1=ax+1与射线y2=bx+2在同一平面直角坐标系中的图象如图所示,则下列说法中①a=2b;②m=4;③点A的坐标为(2,3),正确的( )
已知射线y1=ax+1与射线y2=bx+2在同一平面直角坐标系中的图象如图所示,则下列说法中①a=2b;②m=4;③点A的坐标为(2,3),正确的( )| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 ①把点A坐标,点(4,m)代入射线y1=ax+1和y2=bx+2分别求得a、b,进一步判断即可;
②把x(4,m)代入y2=bx+2求得m的数值即可;
③联立方程组,求得两个函数的交点坐标,进一步判定即可.
解答 解:①把点A坐标,点(4,m)代入射线y1=ax+1和y2=bx+2得
$\left\{\begin{array}{l}{3a+1=4b+2}\\{2a+1=2b+2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=1}\\{b=\frac{1}{2}}\end{array}\right.$,
则a=2b正确;
②把(4,m)代入y2=$\frac{1}{2}$x+2,得m=4,正确;
③由题意得
$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{1}{2}x+2}\end{array}\right.$
解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,
所以点A的坐标为(2,3),正确.
因此①②③都正确.
故选:D.
点评 此题考查两条直线相交的问题,待定系数法求函数解析式,图象上点的坐标特征,根据图象,找出特殊点,建立方程组求得a、b的数值是解决问题的关键.

练习册系列答案
相关题目
11.目前我国年可利用的淡水资源总量为27500亿立方米,人均占有量居全世界第110位,因此我们要节约用水,27500亿这个数用科学记数法表示为( )
| A. | 2.75×1013 | B. | 2.75×1012 | C. | 2.75×1011 | D. | 2.75×1010 |

 (a、b均为正数),字母的值都扩大为原来的2倍,则分式的值( )
(a、b均为正数),字母的值都扩大为原来的2倍,则分式的值( ) C. 不变 D. 缩小为原来的
C. 不变 D. 缩小为原来的
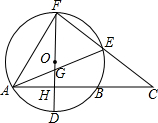 如图,⊙O的直径FD⊥弦AB于点H,E是$\widehat{BF}$上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.
如图,⊙O的直径FD⊥弦AB于点H,E是$\widehat{BF}$上一动点,连结FE并延长交AB的延长线于点C,AB=8,HD=2.