Question

15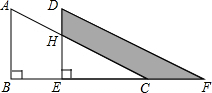．如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到△DEF的位置，AB=10，DH=4，平移距离为6，则阴影部分的面积48．

Answer 1

分析 根据平移的性质可知：AB=DE，BE=CF；由此可求出EH和CF的长．由于CH∥DF，可得出△ECH∽△EFD，根据相似三角形的对应边成比例，可求出EC的长．已知了EH、EC，DE、EF的长，即可求出△ECH和△EFD的面积，进而可求出阴影部分的面积．

解答 解：根据题意得，DE=AB=10；BE=CF=6；CH∥DF．
∴EH=10-4=6；
EH：HD=EC：CF，
即 6：4=EC：6，
∴EC=9．
∴S_△EFD=$\frac{1}{2}$×10×（9+6）=75；
S_△ECH=$\frac{1}{2}$×6×9=27．
∴S_阴影部分=75-27=48．
故答案为48．

点评 此题考查平移的性质、相似三角形的判定与性质及有关图形的面积计算，有一定的综合性．