题目内容
13.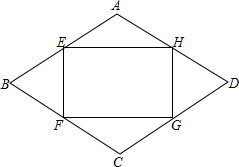 如图:E、F、G、H分别为菱形ABCD的中点,试判断四边形EFGH的形状?并证明.
如图:E、F、G、H分别为菱形ABCD的中点,试判断四边形EFGH的形状?并证明.
分析 根据菱形的性质得到AC⊥BD,根据三角形中位线定理得到EH∥BD,EH=$\frac{1}{2}$BD,FG∥BD,FG=$\frac{1}{2}$BD,得到四边形EFGH是平行四边形,根据平行线的性质证明EF⊥EH即可.
解答 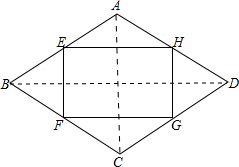 解:四边形EFGH是矩形,
解:四边形EFGH是矩形,
证明:连接AC、BD,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵E、H分别为AB、AD的中点,
∴EH∥BD,EH=$\frac{1}{2}$BD,
同理,FG∥BD,FG=$\frac{1}{2}$BD,EF∥AC,EF=$\frac{1}{2}$AC,
∴EH=FG,EH∥FG,
∴四边形EFGH是平行四边形,
∵EH∥BD,AC⊥BD,
∴AC⊥EH,又EF∥AC,
∴EF⊥EH,
∴四边形EFGH是矩形.
点评 本题考查的是中点四边形的知识,掌握三角形中位线定理、平行四边形的判定、矩形的判定定理和菱形的性质是解题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
3.化简$\frac{|x-2|}{x-2}-\frac{|2-x|}{2-x}$的结果是( )
| A. | 0 | B. | 2 | C. | -2 | D. | 2或-2 |
 如图,正方形的边长为2.分别以正方形的两个顶点为圆心,以2为半径画弧,则阴影部分的周长和面积分别为多少?
如图,正方形的边长为2.分别以正方形的两个顶点为圆心,以2为半径画弧,则阴影部分的周长和面积分别为多少?