题目内容
9. 如图,某客轮以每小时10海里的速度向正东方向航行,到A处时向位于南偏西30°方向且相距12海里的B处发出送货请求,货轮接到请求后即刻沿着北偏东某一方向以每小时14海里的速度出发,在C处恰好与客轮相逢,试求货轮从出发到客轮相逢所用的时间.
如图,某客轮以每小时10海里的速度向正东方向航行,到A处时向位于南偏西30°方向且相距12海里的B处发出送货请求,货轮接到请求后即刻沿着北偏东某一方向以每小时14海里的速度出发,在C处恰好与客轮相逢,试求货轮从出发到客轮相逢所用的时间.
分析 如图,由题意,∠ABF=30°,AB=12海里,推出AF=6海里,BF=6$\sqrt{3}$海里,设货轮从出发到客轮相逢所用的时间为t,则AC=10t海里,BC=14t海里,在Rt△BFC中,根据BF2+CF2=BC2,列出方程即可解决问题.
解答 解:如图,由题意,∠ABF=30°,AB=12海里,
∴AF=6海里,BF=6$\sqrt{3}$海里,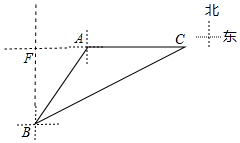
设货轮从出发到客轮相逢所用的时间为t,则AC=10t海里,BC=14t海里,
在Rt△BFC中,∵BF2+CF2=BC2,
∴(6$\sqrt{3}$)2+(6+10t)2=(14t)2,
整理得4t2-5t-6=0,解得t=2或-$\frac{3}{4}$(舍弃),
答:货轮从出发到客轮相逢所用的时间2小时.
点评 本题考查解直角三角形的应用-方向角、等腰三角形的判定、路程、时间、速度之间的关系、勾股定理等知识,解题的关键是掌握方向角的定义,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
8.为了解某小区家庭垃圾袋的使用情况,小亮随机调查了该小区 10 户家庭一周的使用数量,结果如下(单位:个):7,9,11,8,7,14,10,8,9,7.关于这组数据,下列结论错误的是( )
| A. | 极差是 7 | B. | 众数是 8 | C. | 中位数是 8.5 | D. | 平均数是 9 |
18.下列说法中,正确的是( )
| A. | 1的平方根是1 | B. | -1是1的平方根 | C. | 8的立方根是±2 | D. | $\sqrt{9}$=±3 |
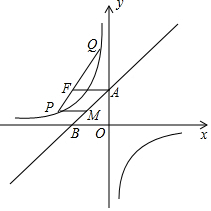 如图,直线y=x+2交y轴、x轴于点A,B两点,点F的坐标为(-2,2),双曲线y=$\frac{k}{x}$过线段AF的中点,在双曲线y=$\frac{k}{x}$(x<0)上取一点P,连接PF并延长交双曲线于点Q,过P点作x轴的平行线交直线AB于点M.
如图,直线y=x+2交y轴、x轴于点A,B两点,点F的坐标为(-2,2),双曲线y=$\frac{k}{x}$过线段AF的中点,在双曲线y=$\frac{k}{x}$(x<0)上取一点P,连接PF并延长交双曲线于点Q,过P点作x轴的平行线交直线AB于点M.
 如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts.
如图,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从点B出发以2cm/s的速度向点A运动,点Q从点A出发以1cm/s的速度向点C运动,设P、Q分别从点B、A同时出发,运动的时间为ts.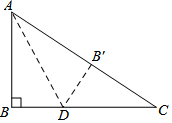 如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将三角形ABC折叠,使AB落在斜边AC上得到线段AB',折痕为AD,则BD的长为3.
如图所示,有一块直角三角形纸片,两直角边AB=6,BC=8,将三角形ABC折叠,使AB落在斜边AC上得到线段AB',折痕为AD,则BD的长为3.