题目内容
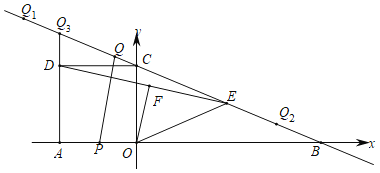
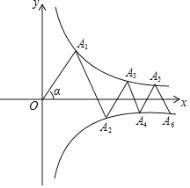
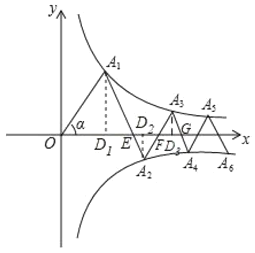
【题目】如图,点A1、A3、A5…在反比例函数y=![]() (x>0)的图象上,点A2、A4、A6……在反比例函数y=-
(x>0)的图象上,点A2、A4、A6……在反比例函数y=-![]() (x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为________________________________.(用含n的式子表示)
(x>0)的图象上,∠OA1A2=∠A1A2A3=∠A2A3A4=…=∠α=60°,且OA1=2,则An(n为正整数)的纵坐标为________________________________.(用含n的式子表示)
【答案】(-1)n+1![]() (
(![]() -
-![]() )
)
【解析】
先证明△OA1E是等边三角形,求出A1的坐标,作高线A1D1,再证明△A2EF是等边三角形,作高线A2D2,设A2(x,![]() ),根据OD2=2+
),根据OD2=2+![]() =x,解方程可得等边三角形的边长和A2的纵坐标,同理依次得出结论,并总结规律:发现点A1、A3、A5…在x轴的上方,纵坐标为正数,点A2、A4、A6……在x轴的下方,纵坐标为负数,可以利用(-1)n+1来解决这个问题.
=x,解方程可得等边三角形的边长和A2的纵坐标,同理依次得出结论,并总结规律:发现点A1、A3、A5…在x轴的上方,纵坐标为正数,点A2、A4、A6……在x轴的下方,纵坐标为负数,可以利用(-1)n+1来解决这个问题.
过A1作![]() 轴于D1
轴于D1
![]() ,
,![]()
∴△OA1E是等边三角形
![]()
![]()
![]() 和
和![]()
过A2作![]() 轴于D2
轴于D2
![]()
∴△A2EF是等边三角形
设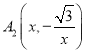 ,则
,则![]()
在![]() 中,
中,![]()
![]()
![]()
解得![]() (舍去),
(舍去),![]()
经检验![]() 是方程的根
是方程的根
![]() ,
,![]()
即A2的纵坐标为![]()
过A3作![]() 轴于D3
轴于D3
同理得![]() 是等边三角形
是等边三角形
设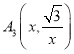 ,则
,则![]()
![]() 中,
中,![]()
![]()
![]()
解得![]() (舍),
(舍),![]()
经检验![]() 是方程的根
是方程的根
![]() ,
,![]()
即A3的纵坐标为![]()
……
∴![]() (n为正整数)的纵坐标为
(n为正整数)的纵坐标为![]()
故答案为:(-1)n+1![]() (
(![]() -
-![]() ).
).

练习册系列答案
相关题目