Question

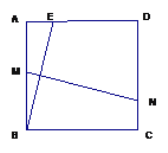
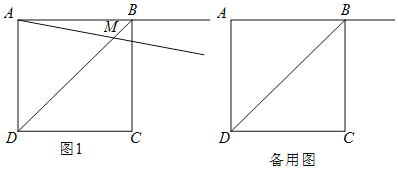
【题目】如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中AF交EC于点M．

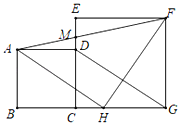
（1）求证：△AHF为等腰直角三角形．

（2）若AB＝3，EC＝5，求EM的长．

Answer 1

【答案】（1）见解析；（2）EM＝

【解析】

（1）通过证明四边形AHGD是平行四边形，可得AH=DG，AD=HG=CD，由“SAS”可证△DCG≌△HGF，可得DG=HF，∠HFG=∠HGD，可证AH⊥HF，AH=HF，即可得结论；
（2）由题意可得DE=2，由平行线分线段成比例可得 ，即可求EM的长．

证明：（1）∵四边形ABCD，四边形ECGF都是正方形

∴DA∥BC，AD＝CD，FG＝CG，∠B＝∠CGF＝90°

∵AD∥BC，AH∥DG，

∴四边形AHGD是平行四边形

∴AH＝DG，AD＝HG＝CD，

∵CD＝HG，∠ECG＝∠CGF＝90°，FG＝CG，

∴△DCG≌△HGF（SAS），

∴DG＝HF，∠HFG＝∠HGD

∴AH＝HF，

∵∠HGD+∠DGF＝90°，

∴∠HFG+∠DGF＝90°

∴DG⊥HF，且AH∥DG，

∴AH⊥HF，且AH＝HF

∴△AHF为等腰直角三角形．

（2）∵AB＝3，EC＝5，

∴AD＝CD＝3，DE＝2，EF＝5．

∵AD∥EF，

∴，且DE＝2．

∴EM＝．