题目内容
【题目】已知反比例函数
，下列结论中不正确的是（ ）
A.图象必经过点 
B.
随
的增大而增大
C.图象在第二，四象限内D.若
，则
【答案】B
【解析】
根据反比例函数图象上点的坐标特点：横纵坐标之积＝k，可以判断出A的正误；根据反比例函数的性质：k＜0，双曲线的两支分别位于第二、第四象限，在每一象限内y随x的增大而增大可判断出B、C、D的正误．
A、反比例函数
，所过的点的横纵坐标之积＝6，此结论正确，故此选项不符合题意；
B、反比例函数，在每一象限内y随x的增大而增大，此结论不正确，故此选项符合题意；
C、反比例函数，图象在第二、四象限内，此结论正确，故此选项不合题意；
D、反比例函数，当x＞1时图象在第四象限，y随x的增大而增大，故x＞1时，6＜y＜0；
故选：B．
练习册系列答案
名校课堂系列答案
相关题目
【题目】如图1，小明用一张边长为
的正方形硬纸板设计一个无盖的长方体纸盒，从四个角各剪去一个边长为
的正方形，再折成如图2所示的无盖纸盒，记它的容积为
．
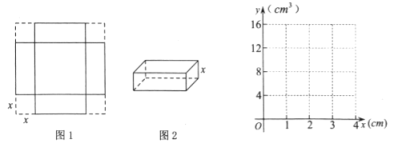
（1）
关于
的函数表达式是__________，自变量的取值范围是___________．
（2）为探究随的变化规律，小明类比二次函数进行了如下探究：
①列表：请你补充表格中的数据：
| 0 | 0．5 | 1 | 1．5 | 2 | 2．5 | 3 |
| 0 | 12．5 | 13．5 | 2．5 | 0 |
②描点：把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点；
③连线：用光滑的曲线顺次连结各点．
（3）利用函数图象解决：若该纸盒的容积超过
，估计正方形边长的取值范围．（保留一位小数）