题目内容
18.用“⊕”定义一种新运算:对于任意有理数a和b,规定a⊕b=ab2+2ab+a.如:1⊕3=1×32+2×1×3+1=16.
(1)求(-2)⊕3的值;
(2)若($\frac{a+1}{2}$⊕3)⊕(-$\frac{1}{2}$)=8,求a的值.
分析 (1)原式利用题中新定义化简,计算即可得到结果;
(2)已知等式利用题中新定义化简,计算即可求出a的值.
解答 解:(1)根据题中新定义得:(-2)⊕3=-2×32+2×(-2)×3+(-2)=-18-12-2=-32;.
(2)根据题中新定义得:$\frac{a+1}{2}$⊕3=$\frac{a+1}{2}$×32+2×$\frac{a+1}{2}$×3+$\frac{a+1}{2}$=8(a+1),
8(a+1)⊕(-$\frac{1}{2}$)=8(a+1)×(-$\frac{1}{2}$)2+2×8(a+1)×(-$\frac{1}{2}$)+8(a+1)=2(a+1),
已知等式整理得:2(a+1)=8,
解得:a=3.
点评 此题考查了有理数的混合运算,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
10.如果多项式mx2-nx-2能因式分解为(3x+2)(x+p),那么下列结论正确的是( )
| A. | m=6 | B. | n=1 | C. | p=-2 | D. | mnp=3 |
8.某商场元旦促销,将某种书包每个x元,第一次降价打“八折”,第二次降价每个又减18元,经两次降价后售价为102元,则所列方程是( )
| A. | x-0.8x-18=102 | B. | 0.08x-18=102 | C. | 102-0.8x=18 | D. | 0.8x-18=102 |
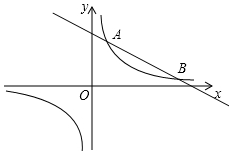 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).