题目内容
12.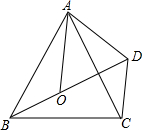 如图,已知O是等边三角形ABC内一点,D是线段BO延长线上一点,且OD=OA,∠AOB=120°,那么∠BDC=60度.
如图,已知O是等边三角形ABC内一点,D是线段BO延长线上一点,且OD=OA,∠AOB=120°,那么∠BDC=60度.
分析 由△ABC为等边三角形可得出AB=AC、∠BAC=60°,由∠AOB的度数利用邻补角互补可得出∠AOD=60°,结合OD=OA可得出△AOD为等边三角形,根据等边三角形的性质可得出AO=AD、∠OAD=60°,根据∠BAO+∠OAC=∠OAC+∠CAD=60°可得出∠BAO=∠CAD,利用全等三角形的判定定理SAS可证出△BAO≌△CAD,根据全等三角形的性质可得出∠ADC的度数,再根据∠BDC=∠ADC-∠ADO即可求出∠BDC的度数.
解答 解:∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°.
∵∠AOB=120°,∠AOD+∠AOB=180°,
∴∠AOD=60°.
又∵OD=OA,
∴△AOD为等边三角形,
∴AO=AD,∠OAD=60°,∠ADO=60°.
∵∠BAO+∠OAC=∠OAC+∠CAD=60°,
∴∠BAO=∠CAD.
在△BAO和△CAD中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAO=∠CAD}\\{AO=AD}\end{array}\right.$,
∴△BAO≌△CAD(SAS),
∴∠ADC=∠AOB=120°,
∴∠BDC=∠ADC-∠ADO=60°.
故答案为:60.
点评 本题考查了等边三角形的判定与性质、全等三角形的判定与性质以及角的计算,通过证明△BAO≌△CAD,找出∠ADC=∠AOB=120°是解题的关键.

练习册系列答案
相关题目
2.甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数是9.2环,方差分别为S甲2=0.54,S乙2=0.61,S丙2=0.50,S丁2=0.63,则射击成绩最稳定的是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
3.实数$\frac{1}{3}$、$\sqrt{3}$、π、$\sqrt{16}$中,无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.已知函数y=-kx(k≠0)的图象经过第一、三象限,(-2,y1)、(-1,y2)、(2,y3)是函数y=(2k-9)x-1图象上的三个点,则y1、y2、y3的大小关系是( )
| A. | y2<y3<y1 | B. | y1<y2<y3 | C. | y3<y1<y2 | D. | y3<y2<y1 |
17.对于$\sqrt{25}$,$\sqrt{2}$×$\sqrt{5}$,(2$\sqrt{5}$)2,$\sqrt{2}$÷$\sqrt{5}$这四个算式,求值结果最大的是( )
| A. | $\sqrt{25}$ | B. | $\sqrt{2}$×$\sqrt{5}$ | C. | (2$\sqrt{5}$)2 | D. | $\sqrt{2}$÷$\sqrt{5}$ |
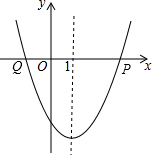 二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,有下列结论:①abc>0;②2a+b=0;③若点P(4,0)在该抛物线上,则4a-2b+c=0;④若(-3,y1),(3,y2)是抛物线上两点,则y1>y2,其中所有正确的结论序号为①②③④.
二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1,有下列结论:①abc>0;②2a+b=0;③若点P(4,0)在该抛物线上,则4a-2b+c=0;④若(-3,y1),(3,y2)是抛物线上两点,则y1>y2,其中所有正确的结论序号为①②③④. 有一个“三阶幻方”如图所示,字母A、B、C代表的数字分别是2、8、6.
有一个“三阶幻方”如图所示,字母A、B、C代表的数字分别是2、8、6.