题目内容
14.以下列各组数作为三角形的三边长,能构成三角形的一组是( )| A. | 2,3,5 | B. | 4,4,8 | C. | 9,10,15 | D. | 6,7,14 |
分析 根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
解答 解:A、3+2=5,不能构成三角形,故此选项不合题意;
B、4+4=8,不能构成三角形,故此选项不合题意;
C、9+10>15,能构成三角形,故此选项符合题意;
D、7+6<14,不能构成三角形,故此选项不合题意.
故选:C.
点评 本题考查了能够组成三角形三边的条件,其实用两条较短的线段相加,如果大于最长的那条就能够组成三角形.

练习册系列答案
相关题目
5.在-2,0,-0.5,3,$\frac{2}{3}$中,负数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.下面实数中无理数是( )
| A. | 0.3333 | B. | π | C. | $\sqrt{16}$ | D. | $\frac{22}{7}$ |
9.已知二次函数y=x2+x+c的图象与x轴的一个交点为(2,0),则它与x轴的另一个交点坐标是( )
| A. | (1,0) | B. | (-1,0) | C. | (2,0) | D. | (-3,0) |
4.关于x的一元二次方程$\frac{1}{2}{x}^{2}$+3x+k=0有两个不相等的实数根,则k的取值范围是( )
| A. | k$<\frac{9}{2}$ | B. | k=$\frac{9}{4}$ | C. | k$≥\frac{9}{2}$ | D. | k$>\frac{9}{4}$ |
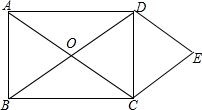 已知矩形ABCD中,对角线AC与BD相交于点O.分别过点D、C作AC、BD的平行线交于点E.
已知矩形ABCD中,对角线AC与BD相交于点O.分别过点D、C作AC、BD的平行线交于点E.