题目内容
如果两个相似三角形的相似比是1：3，则它们的周长的比为（ ）
| A、1：3 | ||
| B、1：9 | ||
C、1：
| ||
D、
|
考点：相似三角形的性质
专题：
分析：根据相似三角形的周长比等于相似比即可解得．
解答：解：∵两个相似三角形的相似比为1：3，
∴它们的周长比为1：3．
故选A．
∴它们的周长比为1：3．
故选A．
点评：此题主要考查相似三角形的性质：相似三角形的周长比等于相似比．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
有理数a、b在数轴上的位置如图，则a+b的值为（ ）| A、大于0 | B、小于0 |
| C、等于0 | D、无法确定 |
若|x+3|+
=0，则x+y的值为（ ）
| y-2 |
| A、1 | B、-1 | C、5 | D、-5 |
如图，在菱形ABCD中，不一定成立的是（ ）| A、四边形ABCD是平行四边形 |
| B、AC⊥BD |
| C、△ABD是等边三角形 |
| D、∠CAD=∠CAB |
下列代数式的意义表述不正确的是（ ）
| A、a+2b的意义是a与2b的和 | ||||
B、x-
| ||||
| C、m（n+3）的意义是m乘以（n+3） | ||||
| D、（a+b）2的意义是a加上b的平方 |
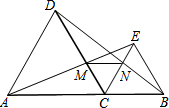如图，点C为线段AB上一动点（不与点A，B重合），在AB同侧分别作等边△ACD和等边△CBE，连结AE与BD，AE与CD交于点M，CE与BD交于点N，连结MN，则对于结论①AE=DB；②EM=BN；③△CMN是等边三角形；④MN∥AB，其中正确结论的个数是（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
若2是方程x2+4x+c=0的一个根，则c的值是（ ）
| A、6 | B、-8 | C、-10 | D、-12 |