题目内容
6.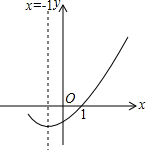 如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0,其中正确的命题是( )
如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0,其中正确的命题是( )| A. | ①②③ | B. | ①③ | C. | ①④ | D. | ①③④ |
分析 根据抛物线经过(1,0),确定a+b+c的符号;根据对称轴方程确定b与2a的关系;根据抛物线与x轴的一个交点和对称轴确定另一个交点,得到ax2+bx+c=0的两根;根据a>0,b>0,c<0,b=2a,确定a-2b+c的符号.
解答 解:∵y=ax2+bx+c经过(1,0),
∴a+b+c=0,①正确;
∵-$\frac{b}{2a}$=-1,∴b=2a,②错误;
∵y=ax2+bx+c经过(1,0),对称轴为x=-1,
∴y=ax2+bx+c与x轴的另一个交点为(-3,0),
∴ax2+bx+c=0的两根分别为-3和1,③正确;
∵a>0,b>0,c<0,b=2a,
∴a-2b+c=-a-b+c<0,④错误,
故选:B.
点评 本题考查的是二次函数图象与系数之间的关系,能够根据开口判断a的符号,根据与x轴,y轴的交点判断c的值以及b用a表示出的代数式是解题的关键.

练习册系列答案
相关题目
20.若a与b互为相反数.则给出的下列关系正确的是( )
| A. | a=b | B. | a=-b | C. | a=1,b=-1 | D. | a=0,b=0 |
17.已知点P(2a-3,a+1)在第二象限,则a的取值范围是( )
| A. | a>$\frac{3}{2}$ | B. | a<-1 | C. | -1<x<$\frac{3}{2}$ | D. | 1<a<$\frac{3}{2}$ |
15. 如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )
如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )
 如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )
如图,圆O中,圆弧AB=圆弧AC,∠C=80°,则∠A=( )| A. | 40° | B. | 30° | C. | 20° | D. | 50° |
16.某校八(1)班50名学生参加市数学质量监控考试,全班学生的成绩统计如下表:
请根据表中提供的信息解答下列问题:
(1)该班学生考试成绩的众数是88;
(2)该班学生考试成绩的中位数是86;
(3)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中游偏上水平?试说明理由.
| 成绩(分) | 71 | 74 | 78 | 80 | 82 | 83 | 85 | 86 | 88 | 90 |
| 人数 | 1 | 2 | 3 | 5 | 4 | 5 | 3 | 7 | 8 | 4 |
(1)该班学生考试成绩的众数是88;
(2)该班学生考试成绩的中位数是86;
(3)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中游偏上水平?试说明理由.
 如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是点N.
如图,在6×4方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是点N.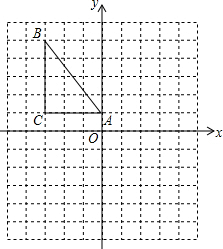 如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,在如图的坐标系中,点A的坐标为(0,1),点B的坐标为(-3,5),AC与x轴平行.
如图,已知Rt△ABC中,∠C=90°,AC=3,BC=4,在如图的坐标系中,点A的坐标为(0,1),点B的坐标为(-3,5),AC与x轴平行.