题目内容
15.抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-3,18),B(2.5,12.5),则关于x的方程ax2-bx-c=0的解为x1=-3,x2=2.5.分析 根据二次函数图象与一次函数图象的交点问题得到方程组,于是易得关于x的方程ax2-bx-c=0的解即可.
解答 解:∵抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(-3,18),B(2.5,12.5),
∴方程组$\left\{\begin{array}{l}{y=a{x}^{2}}\\{y=bx+c}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=-3}\\{y=18}\end{array}\right.$,$\left\{\begin{array}{l}{x=2.5}\\{y=12.5}\end{array}\right.$,
即关于x的方程ax2-bx-c=0的解为x1=-3,x2=2.5.
故答案为x1=-3,x2=2.5.
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$.也考查了二次函数图象与一次函数图象的交点问题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
5.已知-3xy2m+3n与5x2n-3•y8的和是单项式,则m、n的值分别是( )
| A. | 2,1 | B. | 1,1 | C. | 1,3 | D. | 1,2 |
3. 数轴上与1的距离等于2个单位的点表示的数是( )
数轴上与1的距离等于2个单位的点表示的数是( )
 数轴上与1的距离等于2个单位的点表示的数是( )
数轴上与1的距离等于2个单位的点表示的数是( )| A. | 0和2 | B. | -1和2 | C. | -1和3 | D. | -2和2 |
20.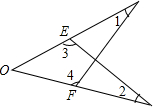 如图,∠1=∠2,3=∠4,OE=OF,则图中全等三角形有( )
如图,∠1=∠2,3=∠4,OE=OF,则图中全等三角形有( )
 如图,∠1=∠2,3=∠4,OE=OF,则图中全等三角形有( )
如图,∠1=∠2,3=∠4,OE=OF,则图中全等三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
7.全国首届青运会在福州举行,下列体育图标中,可以看是中心对称图形的是( )
| A. |  皮筏艇 | B. |  花样游泳 | C. |  自行车 | D. |  柔道 |
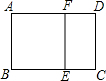 如图,已知矩形ABCD中,AD>AB,在矩形ABCD内作正方形ABEF,若四边形CEFD与矩形ABCD相似,且AB=2,则AD的长为$\sqrt{5}$+1.
如图,已知矩形ABCD中,AD>AB,在矩形ABCD内作正方形ABEF,若四边形CEFD与矩形ABCD相似,且AB=2,则AD的长为$\sqrt{5}$+1.