题目内容
4．
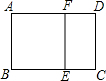如图，已知矩形ABCD中，AD＞AB，在矩形ABCD内作正方形ABEF，若四边形CEFD与矩形ABCD相似，且AB=2，则AD的长为$\sqrt{5}$+1．
分析 根据相似三角形的性质得到F是AD的黄金分割点，根据黄金比值计算即可．
解答 解：∵四边形CEFD与矩形ABCD相似，
∴$\frac{FD}{CD}$=$\frac{CD}{AD}$，
∴CD2=DF•AD，
即AF2=DF•AD，
∴F是AD的黄金分割点，
∴AF=$\frac{\sqrt{5}-1}{2}$AD，又AF=AB=2，
∴AD=$\sqrt{5}$+1，
故答案为：$\sqrt{5}$+1．
点评 本题考查的是相似多边形的性质，掌握相似多边形的性质为：对应角相等；对应边的比相等是解题的关键．
练习册系列答案
相关题目
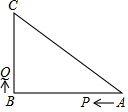如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其 中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．
19．已知函数y=$\frac{5}{x}$经过点P1（x1，y1），P2（x2，y2），如果y1＜y2＜0，那么（ ）
| A． | x2＜x1＜0 | B． | x1＜x2＜0 | C． | x2＞x1＞0 | D． | x1＞x2＞0 |
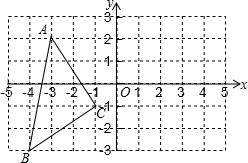如图：在平面直角坐标系中A（-3，2），B（-4，-3），C（-1，-1）．