题目内容
6.计算:(1)3-2-($\sqrt{3}$-2)0-$\sqrt{4}$+|-1|
(2)$\frac{a}{{a}^{2}-{b}^{2}}$-$\frac{4b}{{a}^{2}-{b}^{2}}$+$\frac{3a}{{a}^{2}-{b}^{2}}$
(3)($\frac{1}{a}$+$\frac{1}{b}$)÷$\frac{{a}^{2}-{b}^{2}}{ab}$
(4)$\frac{x-1}{x+1}$+$\frac{4x}{{x}^{2}-1}$.
分析 (1)首先计算乘方,计算绝对值,然后进行加减计算即可;
(2)利用同分母的分式的加减法则即可求解;
(3)首先计算括号内的式子,然后把除法转化为乘法,进行乘法计算即可;
(4)首先进行通分,然后进行加减计算即可.
解答 解:(1)原式=$\frac{1}{9}$-1-2+1=-$\frac{17}{9}$;
(2)原式=$\frac{a-4b+3a}{{a}^{2}-{b}^{2}}$=$\frac{4(a-b)}{(a+b)(a-b)}$=$\frac{4}{a+b}$;
(3)原式=$\frac{a+b}{ab}$•$\frac{ab}{(a+b)(a-b)}$=$\frac{1}{a-b}$;
(4)原式=$\frac{(x-1)^{2}}{(x+1)(x-1)}$+$\frac{4x}{(x+1)(x-1)}$=$\frac{(x-1)^{2}+4x}{(x+1)(x-1)}$=$\frac{(x+1)^{2}}{(x+1)(x-1)}$=$\frac{x+1}{x-1}$.
点评 本题主要考查分式的混合运算,通分、因式分解和约分是解答的关键.

练习册系列答案
相关题目
11.若△ABC≌△DEF,∠A=∠D,∠C=∠F,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
| A. | 5 | B. | 8 | C. | 7 | D. | 5或8 |
18.计算:(x4)2÷x2的结果是( )
| A. | x3 | B. | x4 | C. | x5 | D. | x6 |
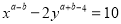 是二元一次方程,那么
是二元一次方程,那么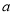 、
、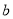 的值分别是( )
的值分别是( )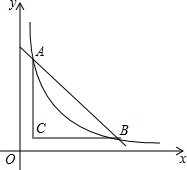 如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$),处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+$\frac{9}{2}$与双曲线y=$\frac{m}{x}$(m>0)的交点
如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$),处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+$\frac{9}{2}$与双曲线y=$\frac{m}{x}$(m>0)的交点